Ideal Gas Law Equation
Ideal gas law or perfect gas law represents the mixed relationship between pressure, volume, and temperature of hypothetical ideal gases for learning the physical properties of the gas molecule in physics or chemistry. The mathematical expression of the ideal gas law equation, PV = nRT, where R = universal gas constant calculated in various units. Such an ideal gas law formula or equation was first derived by Benoît Paul Émile Clapeyron in 1834 by combining empirical Boyle’s, Charles’s, Avogadro’s, and Gay-Lussac’s laws. The ideal gas equation combines state variables of gases in terms of the universal or ideal gas constant (R). The ideal gas law formula and derivation can be used in the solution of a problem related to pressure, volume, temperature, diffusion or effusion, concentration, and the number of gas molecules per unit volume or density of a gas.

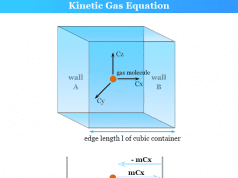
The kinetic gas equation derived by August Krönig and Rudolf Clausius can also be used to formulate an ideal gas law formula. An ideal gas is a gas that obeys the ideal gas law under all conditions of temperature and pressure. However, in reality, it is not true for any gases. Therefore, an ideal gas is a hypothetical gas containing identical particles of negligible volume with no intermolecular attraction.
Four thermodynamics variables (pressure, volume, temperature, and mole number) are used to derive the ideal gas equation from various gas laws. Some of these depend on the mass of the system while others are independent of the mass.
In thermodynamics, the property which proportional to the mass of the system is called the extensive property while which is independent of the mass of the system is called the intensive property. In an ideal gas law equation, the volume is an intensive property but temperature and pressure are extensive properties.
Formula of Ideal Gas Law
Boyle’s law, Charles’s law, and Avogadro’s law give the general derivation formula of the ideal or perfect gases. Mathematical derivation of these laws are,
From Boyles’s law: V ∝ 1/P, when n and T are constant.
Charles law, V ∝ T, when n and P are constant.
From Avogadro’s law, V ∝ n, when P and T are constant.
When all the variables of gas laws are taken into account, we find the mathematical derivation of the ideal gas law equation,
V ∝ nT/P
or, V = RnT/P
∴ PV = nRT
Where, P = pressure,
V = volume,
T = temperature,
n = amount of substance or gas in mole, and
R = ideal gas constant or universal gas constant
Therefore, the derivation of the ideal gas law equation provides the relation between pressure, volume, temperature, and composition of gases. It states that the product of the pressure and the volume of a given mole of a hypothetical ideal gas molecule is equal to the product of kelvin temperature, universal or ideal gas constant, and mole number.
The ideal gas law equation is found to hold the most satisfaction when pressure is low or tense to zero. At ordinary temperature and pressure, the equation is found to deviate about 5%. Therefore, the real or Van der Waals equation obeys the ideal gas law only at low pressures and very high temperatures.
Ideal Gas Law Units
We can use various units of pressure, volume, temperature, and mole number to derive the unit of universal gas constant from the formula of the ideal gas law. Commonly, we used CGS and SI units of such variables to derive universal gas constant.
| Variable | CGS Unit | SI Unit | Other Unit |
| Universal gas constant | erg K−1 mol−1 | J K−1 mol−1 | lit atm K−1 mol−1 |
| Pressure | dyne cm−2 | Pascal or N m−2 | atm |
| Volume | cm3 | m3 | lit |
| Temperature | K | K | K |
| Mole number | mol | mol | mol |
Universal Gas Constant Value
The value of universal gas constant R depends on the amount of gas in the system but does not depend on the nature of the gas. Universal constant values and unit dimension can be calculated from the ideal gas law formula.
The ideal gas equation for n mole gas is,
PV = nRT
At NTP or STP, 1 mole of gases at 1 atmosphere pressure occupied 22.4 liters of volume.
Therefore, the value of the universal gas constant from the ideal gas equation,
R = PV/nT
= (1 atm × 22.4 lit)/(1 mol × 273 K)
∴ R = 0.082 lit atm mol−1 K−1
Universal Gas Constant in CGS Unit
In the CGS system, pressure is expressed in dyne cm−2 and volume is expressed in cm3.
From the formula, pressure (P) = hdg
where h = 76 cm of Hg,
d = density of Hg = 13.6 g cm−3,
g = acceleration due to gravity = 981 cm s−2
∴ P = 1 atm = 76 cm × 13.6 g cm−3 × 981 cm s−2
= 76 × 13.6 × 981 dyne cm−2
Again, volume (V) = 22.4 liters
= 22.4 × 103 cm3
Putting the values of P, V, T, and n in an ideal gas law equation, we can give the value of the universal gas constant (R).
∴ R = (7.6 × 13.6 × 981 × 22.4 × 103)/(1 × 273)
= 8.314 × 107 dyne cm2 mol−1 K−1
Again, dyne cm2 = erg
∴ R = 8.314 × 107 erg mol−1 K−1
Universal Gas Constant in SI Unit
From the value of the universal constant (R) in the CGS system, we can derive the value of R in the SI system.
R = 8.314 × 107 erg mol−1 K−1
Again, 1 J = 107 erg
Therefore, the universal constant value in the SI unit,
= 8.314 J mol−1 K−1
Again from the specific heat relation,
4.18 J = 1 calorie
Therefore, the universal gas constant,
R = (8.314/ 4.18) cal mol−1 K−1
= 1.987 calories mol−1 K−1
≃ 2 calories mol−1 K−1
From the ideal gas equation,
R = PV/nT
= (1 bar × 22.711 dm3)/(1mol × 273.15 K)
= 0.08314 bar dm3 mol−1 K−1
It is another SI unit of universal gas constant (R) derived from the ideal gas law formula.
Ideal Gas Law Constant
The ideal gas law constant is a proportionality constant that is obtained during the formulation of the ideal gas equation.
The formula for n mole ideal gases,
PV = nRT
or, R = PV/nT
From the above formula, the unit of universal gas constant,
R = (pressure × volume)/(amount of gas × temperature)
Again, the unit of pressure = force length−2
Similarly, the unit of volume = length3
Therefore, the unit of R = (force × length−2 × length3)/(amount of gas × temperature) = (force × length)/(amount of gas × temperature)
From the relation, work or energy = force × length
Therefore, the unit of R = (work or energy)/(amount of gas × temperature).
In learning chemistry or physics, the dimensions R obtained from this ideal gas law equation derivation is equal to energy or work per mole per kelvin. Therefore, R represents the amount of work or energy that can be obtained from one mole of gas when its temperature is raised by one kelvin.
Density From Ideal Gas Law
The ideal gas law formula for n mole gas,
PV = nRT
Again, n = m/M
where m = mass of the gas,
M = molar mass
∴ PV = (m/M) × RT
or, P = (m/V) × (RT/M)
From the above formula,
m/V = d = density
∴ P = dRT/M
Therefore, the ideal gas law formula or equation is used to find out the density of gases from the known molar mass of gases.
Number of Molecules Per Unit Volume
The ideal gas equation for n mole gases,
PV = nRT = (N/N0) × RT
Again N = N/NA
Here N = number of gas molecules present
NA = Avogadro number = 6.022 × 1023
From the above relation,
P = (N/V) × (R/N0) × T
∴ P = N′KT
Here, N′ = number of molecules per unit volume
k = Boltzmann constant = R/NA
= 1.38 × 10−16 erg molecules−1 K−1
Problem: Using the ideal gas equation, estimate the number of gaseous molecules left in a volume of 1 ml if it is pumped out to give a vacuum of 7.6 × 10−3 mm of Hg at 0°C.
Solution: Volume (V) = 1 ml = 10−6 dm3
Pressure (P) = 7.6 × 10−3 mm Hg
= 1.01235 × 10-3 kPa.
Therefore, the number of gas molecules,
N’ = (1.01235 × 10−3)/(1.38 × 10−9 × 273)
= 2.68 × 10−11
How to Find Total Pressure Using Ideal Gas Law
According to Dalton’s law of partial pressure, the total pressure of a mixture of gases is equal to the sum of partial pressure. Let a gas mixture contain n1 mole of gas A, n2 mole of gas B, and n3 mole of gas C.
∴ Ptotal = p1 + p2 + p3
If the gases present in the mixture behave ideally, the ideal gas equation is used to find out the total pressure of the gas mixture.
When we write the ideal gas law formula for each gas we have, p1V = n1RT, P2V = n2RT, and P3V = n3RT
From the above three equations,
(p1 + p2 + p3)V = (n1 + n2 + n3)RT
∴ Ptotal = ntotalRT
The fractions n1/ntotal, n2/ntotal, and n3/ntotal are called the mole fractions of the A, B, and C gases respectively. The total pressure of a gas mixture derived from the ideal gas equation is used for the calculation of the mixed pressure for different gases like oxygen, nitrogen, carbon dioxide, hydrocarbon, etc.
Example of Ideal Gas Law Problem with Solution
Problem: Determine the value of gas constant R when pressure is expressed in Torr and volume in dm3.
Solution:
From the relation, 1.01325 bar = 760 Torr
Therefore, R = (0.08314 × 760)/1.01325 Torr dm3 mol−1 K−1
= 62.36 Torr dm3 mol−1 K−1
Problem: The density of ammonia at 5 atmosphere pressure and 30°C temperature is 3.42 g lit−1. How can we calculate the molar mass of ammonia from the ideal gas equation?
Solution:
From the density formula from the ideal gas equation,
P = dRT/M
or, M = dRT/P
Here, d = 3.42 g lit−1
R = 0.082 lit atm mol−1 K−1
T = 303 K
P = 5 atm
Therefore, the molecular mass of ammonia,
MNH3 = (3.42 × 0.082 × 303)/5
= 16.99 g mol−1
≃ 17 g mol−1
Problem: At 50 °C, an ideal gas mixture containing 2 g methane gas (organic compound) and 3 g carbon dioxide gas molecules in a vessel of 5 liter capacity. How can find out the total pressure of the gas mixture?
Solution: From the above problem,
Mole number of methane (nCH4) = 2/16 = 0.125
Mole number of carbon dioxide (nCO2) = 3/44 = 0.0682
Hence total moles,
ntotal = (nCH4 + nCO2)
= (0.125 + 0.0682)
= 0.1932.
Therefore, the total pressure of the gas mixture from the ideal gas equation,
Ptotal = (ntotal × RT)/V
= (0.1932 × 0.082 × 323)/5
= 5.30 atm
Frequently Asked Questions
What is the ideal gas law?
The ideal gas law gives us a relation between pressure, temperature, and volume of a given mass of a gas. Therefore, it states that the product of the pressure and the volume of a given mole of a hypothetical ideal gas molecule is equal to the product of kelvin temperature, universal or ideal gas constant, and mole number.
What is ideal gas equation?
The derivation of ideal gas law for a n-mole hypothetical ideal gas is,
PV = nRT
Where, P = pressure,
V = volume,
T = temperature,
n = amount of substance or gas in moles, and
R = ideal gas constant or universal gas constant = 8.314 J K−1 mol−1
What is R in ideal gas law?
In ideal gas law or equation derivation, R is the universal gas constant because, at any given temperature and pressure, the volume of a gram mole of any gas will be the same.
Which laws can be combined to form the ideal gas law?
Boyles’s, Charles’s, and Avogadro’s laws combined to derive the ideal gas law formula or equation for hypothetical ideal gases.
What is n in ideal gas law?
In the ideal gas equation, n is the amount of substance or number of moles of gas.
What is an ideal gas?
An ideal gas is a gas that obeys gas laws under all conditions of temperature and pressure. However, in reality, it is not true for any gases. Therefore, an ideal gas is a hypothetical gas containing identical particles of negligible volume with no intermolecular attraction.