Slater’s Rule

Slater’s Rule for Calculating Shielding Constant

Slater’s rule is an empirical set of rules in chemistry for calculating the shielding constant or screening constant (σ) and effective nuclear charge (Z_eff) of various electrons present in different orbitals of an atom. The shielding or screening effect decreases the attractive force between the valence shell electron and the nucleus of an atom. Therefore, the shielding effect can affect the chemical trend of periodic table elements.

The empirical rules proposed by John C. Slater in 1930 provide numerical values for the effective nuclear charge in a multi-electron atom. A hydrogen atom contains one electron, hence the hydrogen atom has no shielding electron or effect.

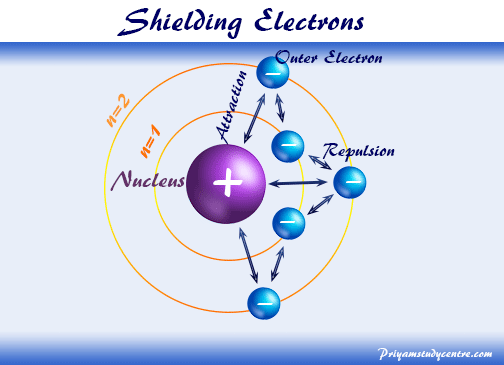
Shielding Electrons

The valence electrons in a multi-electron atom are attracted by the nucleus and repelled by the electrons from inner shells. These attractive and repulsive forces acting on the valence electrons experience less attraction from the nucleus of an atom. Therefore, the inner electrons that shield the higher energy electron are called shielding electrons and the effect is called the shielding effect or screening effect.

In learning chemistry, the larger the number of inner or shielding electrons, the lesser the attraction between the nucleus and outer orbitals electrons. When the number of inner electrons increases, the shielding or screening constant value (σ) also increases.

Screening Constant and Effective Nuclear Charge

Effective nuclear charge (Z_eff) means the net positive charge which affects the attraction of outer electron particles from the nucleus of a polyelectronic atom. Effective nuclear charge is used because the shielding electrons prevent the attraction of the outer orbital electron of an atom.

When the number of inner electrons increases, the shielding or screening constant increases but the effective nuclear charge decreases. Therefore, the decrease of effective nuclear charge affects the chemical properties of the elements, atoms, or molecules and is calculated by Slater’s rule.

The effective nuclear charge (Z_eff ) formula for calculating from Slater’s rule,

Z_eff = Z − σ

Where σ = shielding or screening constant. It can easily be calculated from Slater’s rule.

How to Find Shielding Constant?

Slater proposed some empirical set of rules to find the shielding or screening constant (σ) of various electrons present in different orbitals of an atom or ion.

The electrons are arranged in a sequence of groups in order of increasing principal quantum number (n). In such electron arrangement s and p-orbitals are kept together. Therefore, the electron arrangement order for calculating shielding and screening constant is:

[1s] [2s, 2p] [3s, 3p] [3d] [4s, 4p] [4d] [4f] [5s, 5p], etc.

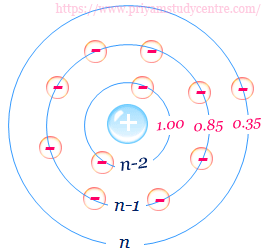
Such arrangement contains three groups such as [1s], [ns, np], and [nd] or [nf]. Each group has a definite shielding constant which is given below in the table,

Group	Other electrons in the same group with principal quantum number n	Electrons in the group with the principal quantum number (n–1)	Electrons in all group(s) with principal quantum number ≤ n–2
[1s]	0.30
[ns, np]	0.35	0.85	1
[nd] or [nf]	0.35	1	1

Slater’s rule for calculating shielding constant for (ns, np) orbitals is slightly different from (nd, nf) orbitals.

s, p Orbitals

Slater’s rules for calculating the screening constant or shielding constant for s, p orbitals electron of an atom or ion are given below:

1. First, we write the electronic configuration of the atom or ion by following order and grouping, [1s] [2s, 2p] [3s, 3p] [3d] [4s, 4p] [4d] [4f] [5s, 5p], [5d], etc.
2. Electrons in a certain (ns, np) level are screened only by electrons of the same energy level and by the electrons of lower energy levels.
3. Electrons lying above the energy level do not screen any electron to any extent. Therefore, the higher energy electrons have no screening effect on the lower energy electrons
4. Electrons of an (ns np) level shield the valence electron in the same group by 0.35 each. It is also true for the electrons of the nd or nf level for electrons in the same group.
5. Electrons belonging to one lower quantum shell or (n−1) shell shield the valence electron by 0.85 each.
6. Electrons belonging to (n−2) or still lower quantum energy levels shield the valence electron by 1.0 each.

Slater’s Rule for Sodium

For calculating the value shielding constant of inner electrons of the sodium atom, the electron configuration according to Slater’s rule, [1s]² [2s, 2p]⁸ [3s]¹.

Therefore, by using Slater’s rule shielding constant and effective nuclear charge for 3s-electron of sodium atom,
σ = (2 × 1) + (8 × 0.85) + (0 × 0.35)
= 8.8

Hence the effective nuclear charge of sodium,
Z_eff = (11 − 8.8)
= 2.2

Shielding or Screening Constant of Sodium and Magnesium Ions

Electron configuration of sodium and magnesium ions according to Slater’s rule:

Na⁺ ion: [1s]² [2s, 2p]⁸
Mg⁺² ion: [1s]² [2s, 2p]⁸

Screening constant for Na⁺ ion,
σ (Na⁺) = (2 × 0.85) + (8 × 0.35)
= 4.5

Similarly, the screening constant for Mg⁺² ion,
σ (Mg⁺) = (2 × 0.85) + (8 × 0.35)
= 4.5

Therefore, the screening and shielding constant for sodium and magnesium ions are similar but the effective nuclear charge of these two ions are different.

Effective nuclear charge for Na⁺ ion = (11 − 4.5) = 6.5
Effective nuclear charge for Mg⁺² ion = (11 − 4.5) = 6.5

Screening Constant of Carbon and Oxygen

Electron configuration of carbon and oxygen according to Slater’s rule for shielding electrons are:

Carbon (atomic number 6): [1s]² [2s, 2p]⁴
Oxygen (atomic number 8): [1s]² [2s, 2p]⁶

The screening constant for carbon,
= (2 × 0.85) + (4 × 0.35)
= 3.10

Similarly, shielding constant of oxygen,
= (2 × 0.85) + (6 × 0.35)
= 3.80

Effective Nuclear Charge of Fluorine

Electron configuration of fluorine and fluoride ion according to Slater’s rule for shielding are:

Fluorine atom (number of electrons 9): [1s]² [2s, 2p]⁷
Fluoride ion (number of electrons 10): [1s]² [2s, 2p]⁸

The shielding constant (σ) for the Fluorine atom,
= (2 × 0.85) + (7 × 0.35)
= 4.15

Similarly, the shielding constant (σ) of fluoride ion,
= (2 × 0.85) + (8 × 0.35)
= 4.5

Therefore, the effective nuclear charge for fluorine atom = (9 − 4.15) = 4.85 and fluoride ion = (9 − 4.5) = 4.5.

Shielding Constant for d or f-Orbital Electron

Slater’s rule for s or p-electron is quite good for estimating the screening constant of s and p-orbital. However, Slater’s rule for d or f-orbital electrons the five and six rules are replaced by new rules for the estimation of screening or shielding effect and effective nuclear charge.

The new rule is all electrons below the nd subshell or nf-subshell contribute 1.0 each towards the screening constant.

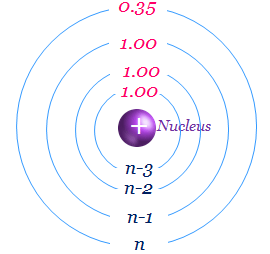
Screening Constant and Z_eff of Vanadium

Vanadium has atomic number 23 and the electron configuration according to Slater’s rules for shielding electrons,
[1s]² [2s 2p]⁸ [3s 3p]⁸ [3d]³ [4s]²

For 4s Electron

The screening constant for 4s electron of vanadium atom,
= (2 × 1.0) + (8 × 1.0) + (8 × 0.85) + (3 × 0.85) + (1 × 0.35)
= 19.7

Hence the effective nuclear charge (Z_eff) for the 4s-electron of the vanadium atom,
= 23 − 19.7
= 3.3

For 3d Electron

Screening constant for 3d electron of the vanadium atom,
= (2 × 1.0) + (8 × 1.0) + (8 × 1.0) + (2 × 0.35)
= 18.70

Hence the effective nuclear charge (Z_eff) for the 3d electron of the vanadium atom,
= (23 − 18.70)
= 4.30

From the above calculation, the screening constant for the 4s electron of vanadium is higher than the 3d electron. Therefore, the 3d electron is more tightly bound than the 4s electron. Hence during ionization, the 4s electron will be lost in preference to the 3d electron.

Screening Constant and Z_eff for Chromium

Chromium has atomic number 24 and the electron configuration according to Slater’s rule for shielding electrons,
[1s]² [2s, 2p]⁸ [3s, 3p]⁸ [3d]⁵ [4s]¹

The screening constant for 4s electron of chromium,
= (2 × 1.0) + (8 × 1.0) + (8 × 0.85) + (5 × 0.85) + (0 × 0.35)
= 21.05

Hence Z_eff for 4s-electron of chromium,
= (24 − 21.05)
= 2.95

The screening constant for 3d-electron of chromium,
= (2×1.0) + (8 × 1.0) + (8 × 1.0) + (3 × 0.85) + (4 × 0.35)
= 19.40

Therefore, Z_eff for 3d-electron of chromium,
= (24 – 19.40)
= 4.60

Effective Nuclear Charge Periodic Trend

The larger the number of electrons in the inner shell, the lesser the attractive force holding the valence electron to the nucleus, and the lower will be the value of ionization energy.

When we move down in the group of the periodic table, the number of shielding electrons increases, and the effective nuclear charge for valence electrons calculated from Slater’s rule decreases. Therefore, the periodic trend of ionization energy and electron affinity is influenced.

• The ionization trends and shielding or screening effect for the group-2 chemical elements, beryllium > magnesium > calcium > strontium > barium. The formation of ionic bonding or polarity trends from Be to Ba is also derived from the effective nuclear charge.
• The magnitude of the electron affinity of periodic table elements is influenced by effective nuclear charge and shielding electrons. In general, electron affinity increses with the decreased screening effect by the inner electrons.

Frequently Asked Questions (FAQs)

What are shielding electrons?

A valence electron in a multi-electron atom is attracted by the nucleus but repelled by the electrons of inner shells.

The combined effect of such attractive and repulsive force acting on the valence electron. Therefore, the valence electron of an atom is shielded by inner-shell electrons.

Which electron has the greatest shielding?

The s-orbital has the greatest shielding effect followed by p, d, and f orbitals because the s-orbital has a higher density of electrons.

Which element has the highest shielding effect?

As we move down a group, the number of inner shells increases and the shielding effect also increses. Therefore, in the alkali metals group, rubidium has the greatest shielding effect and lithium has the least shielding effect.

How to calculate the screening constant of potassium ion?

The electron arrangement of potassium ion is
[1s]² [2s, 2p]⁸ [3s, 3p]⁸

From Slater’s rules, the screening or shielding constant for potassium ion,
= (2 × 1) + (8 × 0.85) + (8 × 0.35)
= 11.6