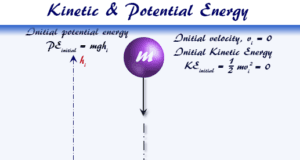
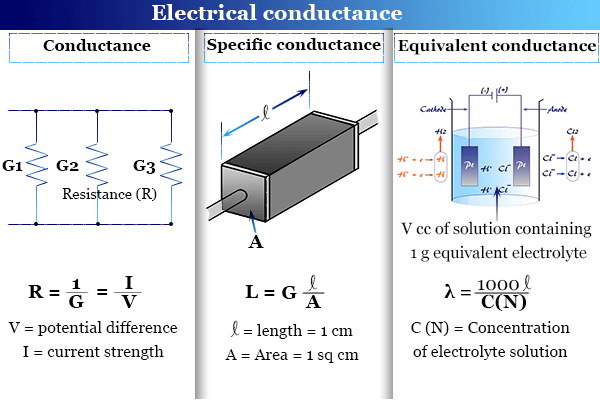
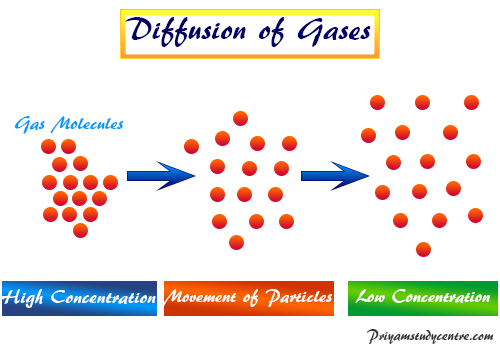
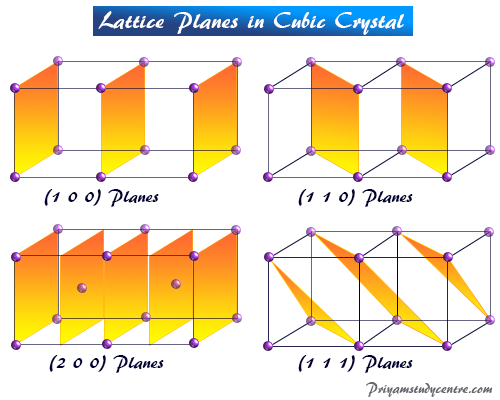
Learning Chemistry
Learning chemistry free online study courses in Priyam Study Centre (PSC) is dedicated to providing organic, inorganic, analytical, spectroscopy, environmental, medicinal, and biochemistry articles for high school and college level science education or classes.
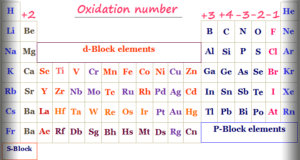
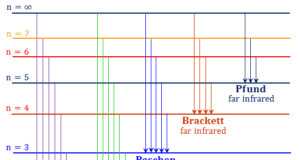
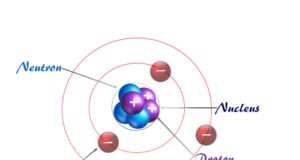
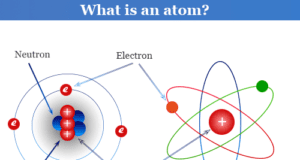
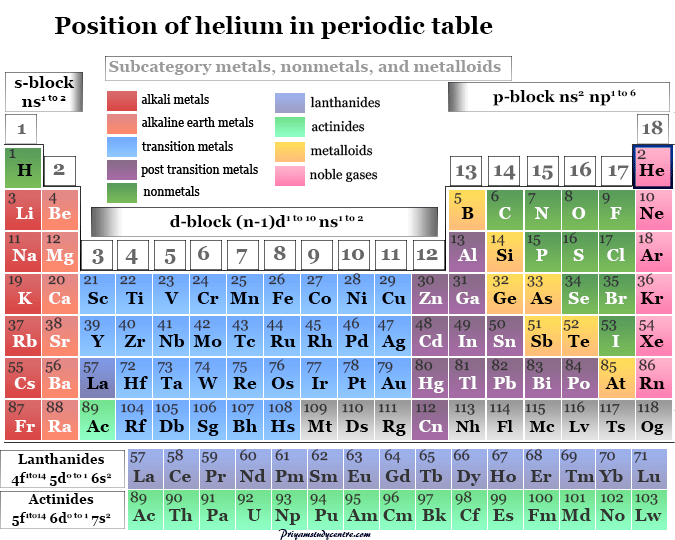
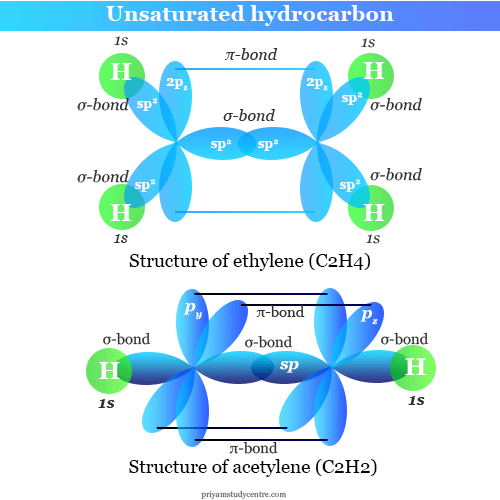
In online learning chemistry, our main aim is to share accurate information about chemical elements, organic and inorganic compounds, analytical techniques, environmental education, spectroscopy, drugs or medicines, and biochemistry to guide high school or college students and researchers in their studies.
We are constantly adding or updating new chemistry articles on our website for students who want to learn from home.
Online Study Chemistry
Online study chemistry or online learning chemistry in PSC not only shares the definition, principles, formula, and application. It also guided you to better learning from home.
It provides questions and answers about chemistry articles in the form of quizzes. These free learning chemistry quizzes on periodic table elements, organic and inorganic compounds, analytical techniques, environmental education, spectroscopy, medicinal chemistry, and biochemistry help the students in their upcoming exams.