Van’t Hoff Equation-Effect of Temperature on Equilibrium Constant
Van’t Hoff equation connecting chemical equilibrium constant (Keq) and temperature by thermodynamics relation of Gibbs-Helmholtz free energy equation. In learning chemistry, the effect of temperature on the equilibrium constant can be easily derive by the Van’t Hoff formula or equation. When the temperature of the system in equilibrium increases, the equilibrium of the chemical reaction shifts in the direction that absorbs heat. If the equilibrium shifts in the forward direction or the concentration of the product molecule increases then more of the reactant molecule is converted into a product. The effect of temperature on the standard chemical equilibrium constant by the Van’t Hoff formula or equation for endothermic and exothermic reactions is given below in the graph.
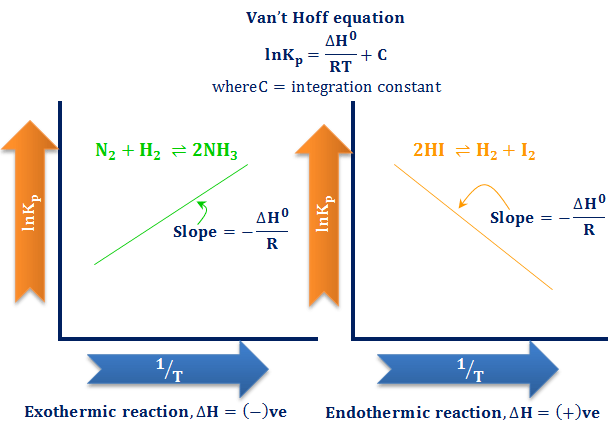
The above plot or graph derived from the Van’t Hoff equation or formula is very effective for calculating the change in enthalpy and entropy of a chemical reaction.
The increases in the extent of reaction lead to increases in the equilibrium constant in physical chemistry which is related mathematically by Van’t Hoff equation.
Derivation of Van’t Hoff Equation
At a given temperature according to Vant Hoff, the equilibrium constant of the chemical reaction remains unaltered. However, the equilibrium constant value varies considerably when the temperature is changed.
Van’t Hoff equation derive mathematically a quantative relation or formula between the equilibrium constant and temperature of a chemical reaction. It can be derived thermodynamically starting from the Gibbs – Helmholtz free energy equation. The mathematical derivation of Van’t Hoff equation is given below in the picture,

The above relation is the differential form of the Van’t Hoff equation. Such a relation also suggests that the greater the value of ΔH0, the faster the equilibrium constant changes with temperature.
Integrated Form of Van’t Hoff Equation
The integrated form of Van’t Hoff isotherm enables us to calculate numerically the shift of equilibrium constant with temperature.
Integration of the above equation,
ln kp = − (ΔH0/RT) + c
where c = integration constant
The integration constant can be calculated from the thermodynamic entropy relation,
ΔG0 = ΔH0 − TΔS0
The equation becomes,
ln kp = − (ΔH0/RT) + (ΔS0/R)
The integrated form of the Van’t Hoff equation at two temperature limits is given below the formula,

where KP1 and KP2 are the equilibrium constants of the Van’t Hoff relation at two different temperatures T1 and T2 respectively.
The determination of KP1 and KP2 at two temperatures helps to calculate the value of the change of enthalpy of the chemical reaction.
The above relation is called Van’t Hoff reaction isobar. Since pressure remains constant during the change of temperature.
Problem: The standard free energy of chemical reaction
2A + B ⇆ 2C at 500 K = 2 k Joule mol−1
Calculate Kp at 500 K for the chemical reaction A + ½B ⇆ C by the Van’t Hoff equation.
Solution: Standard free energy at 500 K for A + ½B → C = 1 kJ mol−1. Therefore, the calculated kp from the Van’t Hoff relation = 1.27.
Van’t Hoff Reaction Isochore
The differential form of Van’t Hoff isochoric equation,
dln kc/dT = ΔU0/RT2
Where ΔU0 = standard heat of reaction at constant volume
The integrated form of the Van’t Hoff equation at two temperature limits is given below the formula,

For the ideal system, ΔU0 = ΔU, and two important assumptions are given from Van’t Hoff isochoric equation.
- The reacting system of the chemical reaction behaves ideally.
- ΔH has been taken independent of temperature during a small range of temperature changes.
Endothermic and Exothermic Reactions
- If a specific heat is absorbed or ΔH0 = positive, the forward direction of the chemical reaction is the endothermic direction and the reverse one is the exothermic direction. The dissociation of hydrogen iodide into hydrogen and iodine is an example of this type of chemical reaction.
- When heat emission or ΔH0 = negative. The forward direction of the chemical reaction is the exothermic direction and the reverse one is the endothermic direction. When the nitrogen atom chemical bonding with the hydrogen atom to form an ammonia molecule, it is an endothermic reaction.
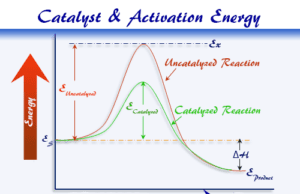
Endothermic vs Exothermic Equilibrium Reactions
Vant Hoff drowns the relation between the equilibrium constant (Keq) with temperature in endothermic and exothermic reactions.
- For an endothermic reaction, ΔH0 > 0, and the right-hand side of the equation is positive. Therefore, it leads to the fact that lnkp increases with increasing temperature.
- For an exothermic reaction, ΔH0 < 0, and the right-hand side of the equation is negative. Therefore, it leads to the fact that lnkp decreases with increasing temperature.
Heat Change in Chemical Reaction
For the ideal system, the heat change is not a function of pressure. However, the standard enthalpy change and normal enthalpy change are equal values for the ideal gases.
The entropy of an ideal gas depends generally on pressure. Therefore, entropy and free energy per mole of reaction in the mixture differ quite substantially from standard entropy and free energy.
Problem: Show that the equilibrium solution for any chemical reaction given by ΔG = 0.
Solution: From the Van’t Hoff reaction isotherm,
ΔG = − RT lnka + RT lnQa
When the chemical solution attains equilibrium,
Qa = ka
∴ ΔG = 0
Effect of Temperature on Equilibrium Constant
Van’t Hoff equation,
ln keq = − ΔH/RT + c
The above equation gives a quantitative expression of the Le-Chatelier principle with temperature and equilibrium constant (Keq).
- During an endothermic reaction, ΔH > 0, an increase in temperature increases the value of keq of the reaction.
- During an exothermic reaction, ΔH < 0, with rising the temperature, keq decreased.
This change of keq provides the calculation of the quantitative change of the equilibrium yield of products. Hence the above statement is in accordance with the Le-Chatelier Principle.
According to Le Chatelier whenever stress is placed on any system in a state of the equilibrium point, the system always reacts in a direction to balance the applied stress.
- If the temperature increases, the system at the equilibrium point will try to move in a direction in which heat is absorbed by reacting or product elements. Therefore, the endothermic reaction favors.
- When the temperature decreases, the system at the equilibrium point will try to move in a direction in which heat is emitted. The exothermic reaction favors according to Van’t Hoff equation or formula and Le Chatelier principle.