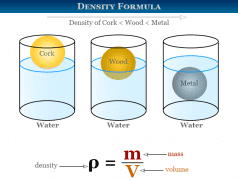
Cubic Crystal System
Crystal lattice or cubic crystal lattice is formed by the orderly arrangement of atoms, ions, or molecules in space or a three-dimensional system. When we consider a cubic crystal system, the lattice point exists in the center, center of each face, and at the corner of a cube and forms three types of unit cells primitive or simple unit cell, body-centered unit cell, and face-centered unit cell. For every crystalline solid, there are three or four lattice planes whose spacing reveals the position or points of the constituents. In learning chemistry or physics, Braggs developed the very simple but useful relation between the wavelengths of the electromagnetic spectrum of x-rays and the spacing between the lattice planes. The Bragg equation states that, nλ = 2d sinθ, where n = 1,2,3, etc, and d = distance between the lattice planes.
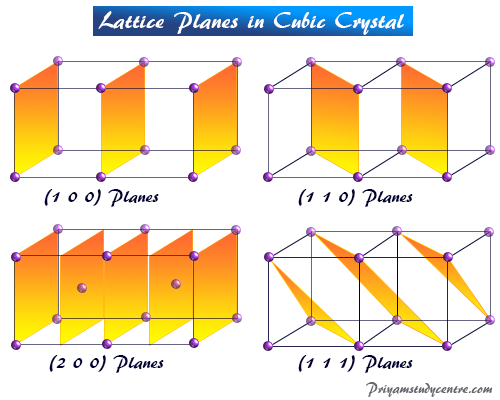
Braggs also developed the character of the line spectrum formed by x-rays which use widely crystallographic studies. For example, cubic sodium chloride formed by ionic bonding, and (100), (110), or (111) planes give the required information about crystal lattice.
The space lattice is divided into a large number of small symmetrical units. When similar points are connected by sets of parallel lines along the three dimensions coordinate axes. These basic units of the space lattice are known as unit cells.
14 Bravais Lattice
Bravais in 1848 shows that all 14 classes of arrangement define all possible forms of the crystalline solid like borax, boric acid, diamond, metallic crystals, etc.
The cubic, tetragonal, orthorhombic, and monoclinic systems have more than one kind of arrangement of the constituents atom, ion, or molecule. These 14 unit cells originated from seven crystal systems known as the Bravais lattice.
Examples of Crystal Lattice
In sodium chloride, the sodium atom loses one electron by ionization to form a sodium ion. Similarly, the chlorine atom has an electron affinity to gain this electron particle to form a chloride ion.
These two ions bind each other by the electrostatic force of attraction to form the ionic body-centered cubic sodium chloride crystal. It liberates lattice energy during the formation of the crystal.
However, ice crystals are formed by hydrogen bonding of water molecules. Different types of force such as Van der Waals, electrostatic, and hydrogen bonding are responsible for the formation of different types of crystals.
Cubic Unit Cells
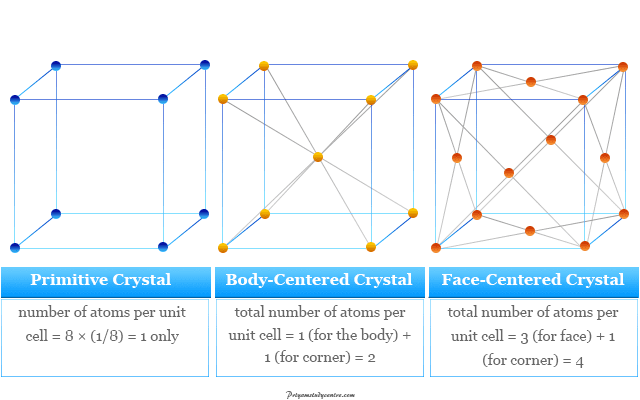
Among these 14 crystal systems, a cubic crystal system forms three types of unit cells
- Primitive or simple unit cell
- Body-centered unit cell
- Face-centered unit cell
Primitive Cubic Unit Cell
In a simple or primitive cubic crystal lattice where atoms are present at the corners only. Each atom is equally shared by eight atoms because each cube contains eight corners. Therefore, the contribution of each atom to the unit cell = 1/8.
The number of atoms per unit cell,
= 8 × (1/8)
= 1 only
Body Centered Cubic Unit Cell
The body-centered atom belongs exclusively to the unit cell. Therefore, the total number of atoms per unit cell,
= 1 (for the body) + 1 (for corner)
= 2
Examples of Body-Centered Cubic Crystal Lattice
The alkali metals like lithium, sodium, potassium, rubidium, and cesium in the periodic table are formed by a body-centered cubic lattice. This type of cubic crystal system possesses one atom at the center and eight atoms at the corner of the cube.
In caesium chloride, the body elements and corner elements are different. All the chlorine ions are at the corner and the caesium cation is at the center of the cubic crystal or vice versa.
Face Centered Cubic Unit Cell
In a face-centered cubic lattice, the atoms are present on the six faces and the eight corners. But face atoms are equally shared by two unit cells.
Therefore, the total number of atoms per unit cell,
= 3 (for face) + 1 (for corner)
= 4
Hence the element density of face-centered unit cells is greater than that of a primitive or body-centered unit cell.
Examples of Face-Centered Cubic Crystal Lattice
The number of periodic tables of chemical elements like copper, silver, gold, nickel, platinum, and solidified inert gases (helium, neon, argon, krypton, xenon) of our environment possess face-centered cubic crystal structures.
Law of Rational Indices
To describe the crystallographic structure of a crystalline solid, we need to discuss the orientation of the plane passing through the lattice point of the cubic crystal. However, the orientation of the lattice plane is described by the intercepts of the plane on the three basis vectors of the lattices.
The intercepts of any plane along the three crystallographic structures are either equal to the ratio of the unit cell or some integral multiple of them. This is known as the law of rotational indices.
Miller Indices for Planes
In learning chemistry, let one plane cut two three-dimensional axes by a and b and the third axis in infinity. Hence the Weiss indices = 1, 1, ∞.
For a better representation of the indexing plane, we avoided infinity. Therefore, considering reciprocal values because infinity is inconvenient for determination. The reciprocal of Weiss indices is called Miller indices.
For example, Weiss indices of (11∞) and (12∞) are represented in Miller indices as (110) and (210) respectively.
How to Calculate Miller Indices?
A cubic system is the simplest type of crystal system. Hence the intercept on the three-axis is equal and all the angles are equal to 90°.
In the simple cubic lattice, the points are at the corner of the cube. The planes that can pass through the lattice point have Miller indices (100), (110), and (111).
- 100 planes cut only on the x-axis but are parallel to the y and z-axis.
- 110 plane cut the x and y-axis but parallel to the z-axis.
- In a cubic crystal lattice, 111 planes cut the x, y, and z-axis.