Nuclear Binding Energy

How to calculate nuclear binding energy?

Nuclear Binding energy can calculate from the expected mass of any nucleus from the knowledge of the nuclear composition like masses of proton and neutron particles.

In chemistry, such binding energy calculation shows that the calculated mass of a nucleus is always greater than the experimentally determined mass. This difference is called the mass defect, mass deficit, or mass decrement of an atom in nuclear chemistry.

Nuclear binding energy curve

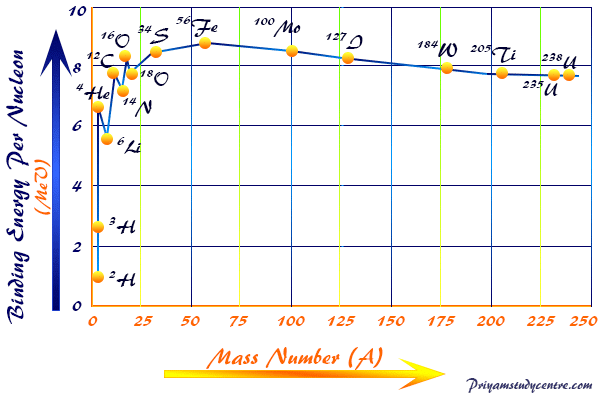
Binding energies vary greatly with the bound particles or the composition of the nucleus of periodic table elements. An idea of the relative stability of the stable nuclei of different chemical elements can be obtained by the plot of the binding energy per nucleon against the mass number of elements.

What is mass defect?

Let an atom has mas number = A and atomic number = Z. The atom contains Z number of proton and (A − Z) number of neutron particles in the nucleus. Therefore, the mass of the atom is expected to, (A − Z)m_n + Zm_p + Zm_e.

But the isotopic mass (M) is usually less than the theoretically calculated value. Therefore the difference is called mass defect equal to the value,
D = (A − Z)m_n + Zm_p + Zm_e − M
= (A − Z)m_n + Zm_H – M.

Where m_n = mass of the neutron, m_p = mass of the proton, m_e = mass of the electron, and mass of hydrogen atom = m_H = m_p + m_e.

Mass defect of helium

For example, the helium nuclei (₂He⁴) have the following data for binding energy and mass defect calculation, the mass of two protons and neutrons = 2.01456 and 2.01743 amu respectively.

Therefore, the total mass,
= (2.01456 + 2.01743)
= 4.03190 amu.

But the actual mass of helium nuclei (₂He⁴) = 4.0015 amu. Hence (4.03190 – 4.00150) = 0.03040 amu is the mass defect of helium. This mass defect is converted or transformed into energy by the Einstein relativity equation in physics or nuclear chemistry.

Binding energy of nucleus

According to the definition of binding energy, the energy required to hold together the individual protons and neutrons of a single nucleus. It is calculated from the loss of mass or mass defect. The mass loss is converted into energy according to the law of mass energy conservation with the Einstein equation, E = mc². 1 amu mass produces 1.492 × 10^-3 erg or 931 MeV of energy.

The energy formula derived from the Einstein mass-energy equation is responsible for holding the constituent particles together. Therefore, the calculated binding energy per nucleus in MeV units = 931 × D.

For examples, the mass defect in the deuterium atom,
= m_p + m_n + m_e − m
= 0.00293.
Therefore, E_B = 931 × 0.00293
= 2.72 MeV

Average binding energy per nucleon

The mass defect for helium atom = 0.03040 amu and E_B = 0.03040 × 931 MeV = 28.3 MeV. But the helium nucleus contains a total of four nuclear particles or nucleons. The average binding energy per particles or nucleon = 1.36 MeV but the mean value = 28.3 MeV/4 = 7.07 MeV.

Atom	Binding Energy (MeV)	Mean EB per Nucleon
7Li	39.27	5.61
12C	92.30	7.69
20Ne	160.00	8.00
209Bi	1630.00	7.80

The mean binding energy formula per particle (proton, and neutron) or nucleons is different in different atoms expressed above the table laying between the values 7.5 to 8.5 plotted against the atomic number of curve or graph.

The plot shows that the binding energy per nucleon rises sharply from the isotopes of hydrogen to the next heavier chemical elements and produces a large amount of energy by bound or fusing together or nuclear fusion.