de Broglie Wavelength Formula
de Broglie wavelength formula proposed by French physicist Louis de Broglie in 1924 derived the relation between Einstein’s mass-energy equation and Planck’s quantum theory. Â de Broglie wave formula suggests that just like a photon, an electron have also both particle and wave properties. His hypothesis suggested that electrons travel in waves, analogous to light with a definite wavelength or frequency. The de Broglie hypothesis could be fitted to derive the relation that the Bohr model proposed.
In physics or chemistry, the combination of Einstein’s mass-energy formula and Planck’s quantum theory is used to derive the de Broglie wavelength relation. It is used to calculate the wavelength and frequency of electromagnetic spectrum radiation. This wavelength relation was tested by Davisson Grammar experiments and Bohr’s theory of hydrogen atoms.
de Broglie Relation Derivation
de Broglie derives a relation to calculate the wavelength of a wave associated with a light particle or photon. This wavelength relation can be derived with the help of the Planck equation and Einstein’s mass-energy formula of matter.
If the wavelength of a light particle = λ, frequency = ν, and energy = E.
From the Planck quantum equation,
E = hν = hc/λ
Here, c = velocity of light,
h = Planck constant = 6.627× 10−27
The Einstien mass-energy relation,
E = m c2
Combining these two relations,
mc = h/λ
or, p = h/λ
where, p = mc = mv = momentum
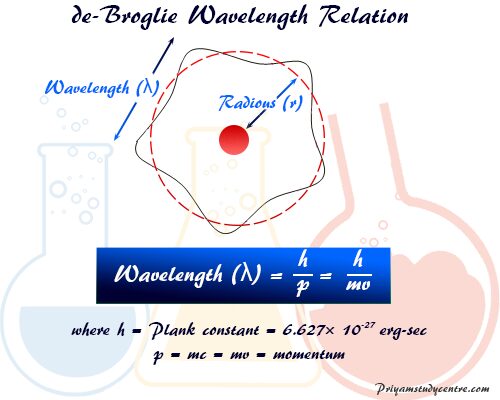
∴ Wavelength (λ) = h/p
de Broglie relation extended light particles to the wave particles of matter and calculated the mass, momentum, wavelength frequency, and energy of an electron. Therefore, when an electron of mass m moves with the velocity v around the nucleus, it forms a wave with the wavelength λ.
From the de Broglie wave formula,
λ = h/p = h/mv
where m = total mass of electron
v = velocity
The above wave formula is called the de Broglie formula and the wavelength is called the de Broglie wavelength. It also shows that the momentum (p) of the moving electron is inversely proportional to the wavelength (λ).
de Broglie Wavelength and Bohr Model
We have seen that Bohr in his model shows that an electron is a particle revolving around the nucleus in a circular orbit. But de Broglie pointed out in 1924 that the electron has a dual character. Therefore, like light, an electron also behaves as a particle and as a wave.
According to de Broglie, the electron is not a solid particle revolving around the nucleus of an atom. It is a standing wave extending around the nucleus of a circular orbit. Angular momentum of moving electrons from Bohr atomic structure,
mvr = nh/2Ï€
or, mv = nh/2Ï€r
where m = mass of an electron,
n = principle quantum number = 1, 2, 3, 4, …
r = radius of the orbital of an atom.
According to de Broglie’s equation
λ = h/mv
or, mv = h/λ
where λ = wavelength of the moving electron.
Combining de Broglie equation and Bohr’s theory
2πr = nλ
From the above formula, it should be suggested that there will be an integral number of wavelengths that must fit into a circular orbit of Bohr. Such an integral number of wavelengths must generate a standing wave.
A standing wave produces a stationary pattern or fixed profile. It does not travel beyond the allowed space.
Experimental Verification
Experimental verification of the de Broglie equation was obtained by Davisson and Germer in 1927. The success comes by diffracting a beam of electrons from the nickel surface. The pattern of electron diffraction obtained by them is similar to that of x-ray diffraction.
The wavelength of electrons obtained from the experiment is identical to the calculated wavelength by the de Broglie relation. In this way, the particle and wave nature of an electron and the quantized nature of the de Broglie relation were established.
de Broglie Wavelength and Kinetic Energy
When the particle-like light photon or electron is subjected to the potential difference V, it acquires a velocity v and generates two types of energies, potential and kinetic energy.
The energy of an electron,
E = Ve = ½ mv2
where e is the charge of an electron.
Again, λ = h/mv
From the above two relations,
wavelength (λ) = h/√2mVe
The above formula is derived from the de Broglie wave equation and kinetic energy is used to calculate the wavelength of a photon or an electron.
