Law of conservation of energy
Law of Conservation of energy or conservation of energy principle in thermodynamics states that the total heat or energy of our universe must remain constant. The relation between heat and work is the origin of the first law of conservation of energy.
The first law of energy conservation in thermodynamics states that energy can neither be created nor be destroyed but may be transferred from one form to another.
In other words, when one form of energy disappears, an exact and same amount of other form appears to maintain the net amount of energy in our universe. Hence a definite quantity of electrical energy is given to be equivalent quantity of heat or mechanical work.
In chemistry or physics, the conservation of energy principle provides the calculation and formula for specific heat change and transfer in cyclic, isothermal, isochoric, and isolated processes in terms of internal energy and work done by the system.
Energy conservation formula
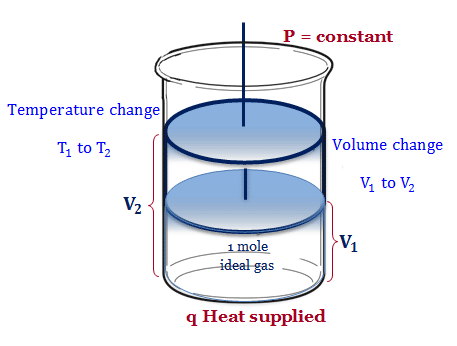
Let q amount of heat supplied to the system containing one mole gas in a cylinder fitted with a frictionless weightless moveable piston. At constant pressure, the gas molecules expand from volume V1 to V2, and the temperature changes from T1 to T2.
According to the 1st law of thermodynamics,
q = dU + w
where dU = change of internal energy
If the work is restricted to pressure volume work or mechanical work,
w = PdV
∴ q = dU + PdV
Heat change in thermodynamics for ideal or real gases derived from the ist law of thermodynamics and ideal gas law or Van der Waals equation. All ideal and real gases obey these energy conservation formulas.
Energy change formula
First law of thermodynamics for cyclic process
Internal energy changes in the cyclic process, dU = 0. Therefore, according to the first law, q = w. Hence from the energy conservation principle, heat is completely converted into work for the cyclic process.
Work done in isothermal process
Internal energy change in the isothermal process for the ideal gas,
dU = ncvdT = 0
∴ q = w
Hence, thermodynamics heat is completely converted into work for the ideal gas in the isothermal process.
Energy change in isochoric process
Volume change in isochoric process, dV = 0.
From the energy conservation principle,
q = dU = ncvdT
Therefore, energy change to an isochoric process only increases the internal energy or temperature of the system.
First law of thermodynamics for isolated system
In an isolated system, neither energy nor matter can be transfer to or from it. Therefore, q = 0 for isolated system. Hence from the energy conservation principle,
w = − dU
Therefore, the isolated system uses internal energy for doing work.
Conservation of energy examples
We often say motor produces work. But in reality, the motor does not give us any work if electrical energy is not supplied to it.
Similarly, electricity is generated by losing some mechanical or thermal energy. The net change of the internal energy of the system and surroundings is zero.
The change of internal energy is independent of the path or way of transformation but heat change and work done are dependent on the path of transformation.
For example, when the element zinc reacts with copper sulfate in the solution, a considerable quantity of heat is produced. But if the same redox reaction takes place in the voltaic cell practically no heat evolved and the internal energy converted into electric work.
If oxidation of the mixture of gasoline or burnt gasoline is in the air the large quantity of heat is produced. But if the same change is carried out in the engine, the combustion pushes out the piston and performs work.
Here engine produces a Lasser quantity of heat than the oxidizing process. Therefore the magnitude and work done very with the condition of the experiment in thermodynamics energy conservation.
