Viscosity of liquids

Measuring Viscosity of Liquids

Viscosity of liquids in chemistry is measuring the resistance to flow exhibited by fluids (liquids or gases) like glycerol, ester, oils, water, alcohol, and ether. The flow of some liquids is slower than the others due to this property. For example, glycerol, ester, and oil flow slowly while water, ether, and alcohol flow rapidly on the solid surface due to viscosity. The former liquids are called high viscous liquids while the latter liquids are called low viscous liquids. The reciprocal of viscosity is called fluidity which measures the flowing tendency of the liquid for learning chemistry and physics. The measurement of viscosity data of fluids is important in the study of biology, chemistry, and physiology. It is also used to deal with various problems in fluid mechanics, especially in paint, ink, colloids, rubber, textiles, etc. Recently it was used in the determination of the molecular weight of polymers. 71 110

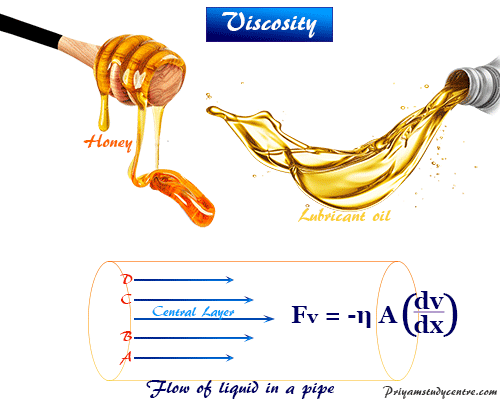
Kinematic Viscosity

Kinematic viscosity in physics is sometimes used in engineering studies for comparing and measuring the properties of different liquids. It is defined as,

Kinematic viscosity = viscosity coefficient (η)/density (ρ)

Kinematic viscosity expressed or calculated in the Stoke unit in honor of the scientist Stoke.

Fluid Flow in Pipes

When the fluid flows within the pipe or cylindrical tube, all the parts of the fluid do not move with equal velocity. A thin layer immediately in contact with the wall of the pipe remains almost stationary.

The velocity of the successive layers from the wall of the pipe increases and remains maximum for the central layer. Therefore, there is a velocity gradient of the flowing liquid,

Velocity gradient = (dv/dx)

Each layer of the liquid surface flowing with a higher velocity experience a retarding effect due to the internal friction of the two layers. The resistance that one part of a fluid flowing with one velocity offers to another part of a fluid flowing with different velocities is known as viscosity.

Due to the continuous movement of gases, there will be an interchange of molecules between two layers. It results in a fraction of the momentum of one layer will pass over the other layer. The net effect can decrease the moment of one layer with respect to another. In order to maintain a uniform velocity gradient, one will have to apply a force acting along the direction of the movement of other layers. Such applied force is used for measuring the viscosity of gases.

The internal friction of liquids is aries due to intermolecular attraction. Molecules in a slower-moving layer try to decrease the velocity of molecules in a faster-moving layer and vice versa. Therefore, some tangential force is required to maintain a uniform velocity in liquids and it will depend on the area of contact between the two layers and the velocity gradient.

Different Types of Fluid Flow

The main types of fluid flow may include,

• Laminar flow
• Streamline flow
• Turbulent flow

Laminar Flow

In Laminar or streamlined flow, the velocity of the discharge of a liquid is low and all the layers of liquid move parallel to each other. The velocity of the fluid (liquid and gas) is mostly the same in magnitude and direction at any particular point.

The streamlines do not cross each other at any point in the flow. Newton’s law of viscous flow is only applicable to the laminar flow of liquids.

Turbulent Flow

When the rate of discharge of moving liquid is high, the condition of streamline flow is not maintained, and turbulent flow is started. The velocity of the liquid at a point varies with time irregularly.

Reynolds Number

A dimensionless quantity, named, Reynolds number (Re) uses to define different types of liquid flow. It has the value,

Re = (dρu/η)

Where, η = viscosity coefficient,
ρ = density,
d = diameter of the tube,
u = velocity of the liquid.

• When Re < 1000, streamline flow occurs.
• When Re ≈ 1000 to 1500, turbulent flow starts.
• When Re > 1500, turbulent flow persists in the liquid.

The capillary tube is used for measuring viscosity to maintain a streamlined flow of liquid since the diameter of the tube is very small.

Factors Affecting Viscosity

The fraction between two layers moving with different velocities originates from the intermolecular attraction in liquid.

Viscosity in the liquid increases with the rise of temperature but in gases, it increases with the increase of temperature. This is due to the different origins of the term viscosity in the liquid and gas phases.

1. In gas, it originates due to the exchange of momentum between two moving layers and no effect of pressure unless it is very low.
2. In liquid, viscosity generally increases with an increase in pressure.

Coefficient of Viscosity Formula

The coefficient η is the measured viscosity of liquids and gases and is defined by Newton’s law of viscous flow in science.

The returning force originates due to internal friction between moving layers with the velocity gradient = (dv/dx) and area = A is expressed by the equation,

Fv = − η A (dv/dx)
where η = symbol of viscosity coefficient of liquid.

According to the above mathematical formula, viscosity is defined as the force per unit area originating between the two layers moving with the unit velocity gradient.

Coefficient of Viscosity Unit and Dimension

• The unit of viscosity coefficient (η) in the CGS system is poise (g cm⁻¹ sec⁻¹).
• In the SI system, the unit of η is Pascal sec (kg meter⁻¹ sec⁻¹).
• The relation between the two units, 1 pascal sec = 10 poise.
• The dimensions of the quantity = [M L⁻¹ T⁻¹].

Effect of Temperature on Viscosity

Intermolecular attraction decreases with increases in temperature. Hence the viscosity of a liquid also decreases by 2 percent with the rise of temperature per degree Celsius. This is due to the fact that at rising temperatures, the average thermal energy of its molecule increases.

The relation of η with temperature is given by,

η = A e^E/RT
where E = activation energy of the viscous flow
A = constant for liquid

In learning chemistry or physics, the measuring of mobility or fluidity (reciprocal of viscosity) of liquids or gases generally follows the Boltzmann energy distribution law,

Fluidity (φ) ∝ e ^−E/RT