Specific Heat Capacity of Gases
Specific heat capacity of gases is defined as the amount of heat required to raise the temperature of one gram of gases by unit degree but per mole of gas is called molar heat capacity or simply heat capacity. Usually, the heat capacity of gases expressed at constant pressure (Cp) and volume (Cv) and energy units is used for its calculation in physics or chemistry. Monoatomic noble gas molecules like helium, neon, and argon when heated in constant volume, the heat supplied will be utilized in increasing the translational kinetic energy because these molecules have no vibrational or rotational energy. Atomic heat is the product of specific heat and the atomic weight of the element. Such formula is used to calculate the heat capacity of many periodic table elements like silver, gold, aluminum, lead, iron, etc.
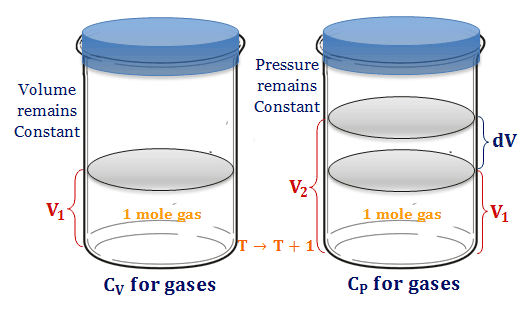
At constant volume, these mono-atomic gases, can not be used any energy to perform mechanical work. But if we heat in constant pressure the gas expands against the piston and does mechanical work.
For polyatomic gases, the supplied heat uses not only translational kinetic energy but also vibrational or rotational energies. Solids also have heat capacities measured from Dulong Petit experimental data that the atomic heat of all crystalline solid elements is the constant quantity and approximately equal to 6.4 calories.
Heat Capacity Units
Specific heat capacity is an extensive property because the amount of heat required to raise temperature depends on the mass of the substances. The unit of specific heat capacity = J K−1 kg−1
Molar heat capacity is an intensive property in thermodynamics having the unit = J K−1 mol−1.
We also use CGS and calorie units to specify the heat capacities of the solid and gaseous substances. But if we mention molar and specific heat then per mole and per gram (g) or kilogram (kg) are used to specify such units.
Formula for Heat Capacity
The amount of thermal energy required to raise the temperature of one gram of a substance by 1°K is called specific heat and for one mole is called molar heat capacity.
Heat Capacity at Constant Pressure Formula
At constant pressure, heat capacity can be defined by the formula,
Cp = M × cp
Here, Cp is measured at constant pressure and cp is their specific heat.
From the above formula, the temperature of one gm-mole of gas raised by one degree at constant pressure is called heat capacity at constant pressure or simply Cp.
Heat Capacity at Constant Volume Formula
Again from the definition, the formula of heat capacity at constant volume,
Cv = M × cv
Here, Cv is measured at constant volume, cv is their specific heat.
Therefore, the temperature of one gm-mole of gas raised by one degree at constant volume is called heat capacity at constant volume or simply Cv.
Heat Capacity in Thermodynamics
Like other thermodynamic properties (internal energy, enthalpy, entropy, and free energy), heat capacity also is the thermodynamic property.
When dq energy is required to increase the temperature dT for one mole of the gaseous substances. The thermodynamic definition of the specific heat capacity,
C = dq/dT
Where dq = path function.
Therefore, the values of heat change depend on the actual process that followed for this measurement. But we can place certain restrictions to obtain precise values of Cp and Cv.
The usual restrictions are at constant pressure and constant volume.
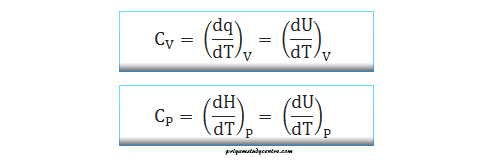
Heat Capacity for Gases
The calculation of Cp or Cv depends on the pressure and volume of gases. The observed quantity in the two operations would be different. Therefore, for measuring heat capacity, the conditions of pressure and volume must be specified.
In learning chemistry and physics, Cp, Cv, and Cp/Cv or γ of some gases at 1 atm pressure and 298 K temperature are given below the table,
| Gas (monoatomic or polyatomic) | Heat Capacity | γ = Cp/Cv | |
| Cp | Cv | ||
| Argon (Ar) | 4.97 | 2.98 | 1.66 |
| Helium (He) | 4.97 | 2.98 | 1.66 |
| Mercury (Hg) | 5.00 | 3.00 | 1.67 |
| Hydrogen (H2) | 6.85 | 4.86 | 1.40 |
| Nitrogen (N2) | 6.96 | 4.97 | 1.40 |
| Oxygen (O2) | 7.03 | 5.03 | 1.40 |
| Carbon dioxide (CO2) | 8.83 | 6.80 | 1.30 |
| Sulfur dioxide (SO2) | 9.65 | 7.50 | 1.29 |
| water (H2O) | 8.67 | 6.47 | 1.34 |
| Methane (CH4) | 8.50 | 6.50 | 1.31 |
Problem: The Cp and Cv of gases are 0.125 and 0.075 cal g−1 K−1 respectively, how to calculate the molecular weight and the gas formula from the specific heat equation? Name the gas if possible.
Solution: M = 40 and ⋎ = 1.66(mono-atomic), Ar(Argon).
Mechanical Work Formula
A monoatomic gas can be heated at constant pressure and constant volume in a cylinder fitted with a piston. When the gas expands against the piston gives mechanical energy.
In order to attain a 1° rise in temperature, the heat supplied should be sufficient to increase the energy of the molecules and also be able to do extra mechanical work. Therefore, Cp is equal to some mechanical energy required for lifting the piston from volume V1 to V2.
CP − CV = mechanical work or energy
= PdV = P(V2 − V1)
= PV2 − PV1
If the gases obey ideal gas law, PV = RT.
Therefore, Cp − Cv = R(T + 1) − RT
or, Cp − Cv = R = 2 calories
Heat Capacity Calculation
For Monoatomic Gas
When monoatomic gases (argon or helium) are heated at constant volume, it is utilized for increasing the kinetic energy of the translation. Since the monoatomic gas molecules can not have any vibrational or rotational motion.
When the volume of the gas remains constant, no heat is used to do any mechanical work. The Kinetic energy for one-mole ideal gases at T temperature,
E = 3PV/2
= 3RT/2
For monoatomic gas (helium or argon), kinetic energy for one (1°) rise in temperature,
ΔE = 3{R(T + 1) − RT}/2
= 3R/2
=3 calories
The heat supplied at a constant volume is equal to the rise in kinetic energy per unit degree rise in temperature.
∴ Cv = ΔE = 3 calories
For one mole of monoatomic gas, the ratio of Cp/Cv is universally expressed by the symbol γ calculated by the following equations,
γ = Cp/Cv
Cp − Cv = R
From the above two equations,
γ = (Cv + R)/Cv
= (3 + 2)/3
= 1.66
For Polyatomic Gas
For polyatomic molecules, the heat supplied is not used only in increasing kinetic energy but also in increasing vibrational or rotational energies. Let x calories be used for increasing vibrational or rotational purposes.
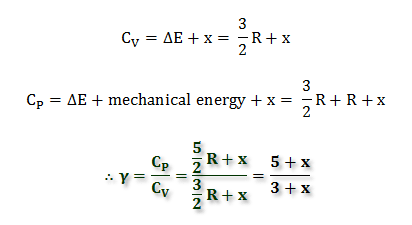
Cp − Cv = 2 calories remain constant for this energy equation but the Cp/Cv calculation differs from gas to gas.
Specific Heat and Heat Capacity
Heat supplied to one gram-mole of a gas kept at a constant volume to increase the temperature by one degree has the Cv for monoatomic or polyatomic gases.
- For monoatomic gases, heat energy is used to increase the translational kinetic energy.
- For polyatomic gases, heat energy is used to increase translational, vibrational, and rotational kinetic energy.
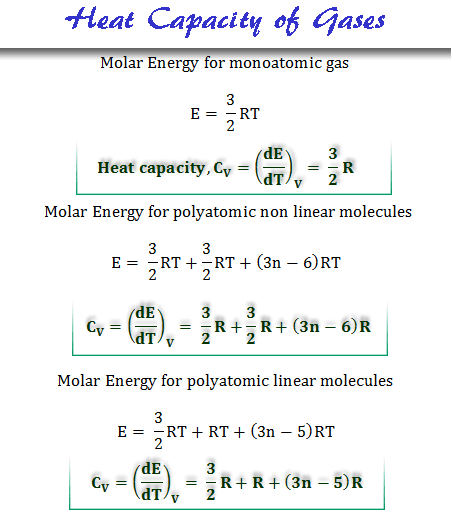
Heat Capacity Values
Experimental and calculation values of Cp and Cv revels due to the following facts. Due to the perfect arrangement of the monoatomic gases,
Cv/R = 1.5.
Therefore, the value of Cp and Cv is independent of temperature over a wide range.
For polyatomic gases, two points of disarrangement were found, the first is always lower than the predicted value and the second is noticeably dependent on temperature. The observed values of heat capacity for polyatomic gases lie between the range of 2.5 to 3.5.
Classical mechanics does not describe the vibrational motion of gas molecules and we use quantum mechanics to describe it. The principle of equipartition is derived from the classical consideration of continuous energy absorption by atoms governed by Maxwell distribution.
Vibrational and rotational energy take place in discrete units, but the measured value of the specific heat of gas or gases is explained only on the basis of the quantum equation.
At high temperatures, the energy levels are quite close and the observed spectrum would be continuous and the heat capacity equation for gas molecules would be valid.