Density Calculation Formula
Density calculation formula for solids, liquids, and gas molecules is the measurement of mass per unit volume at a given temperature and pressure. In chemistry or physics, density is expressed by the symbol ρ or D.
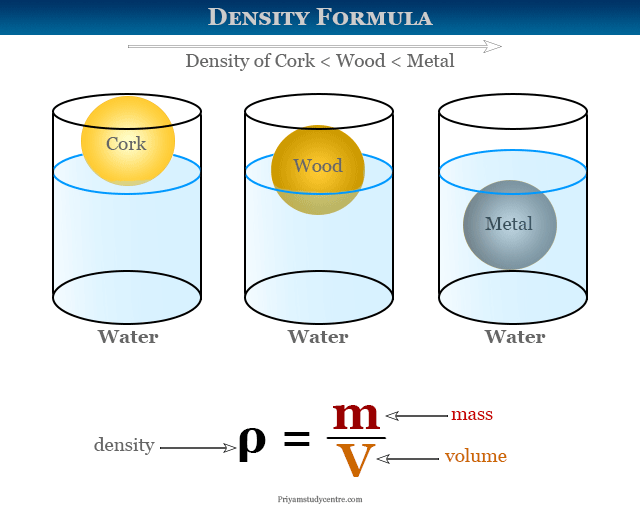
Mathematically density formula can be expressed by,
ρ = m/V
where m = mass of the substance and V = volume.
A standard or normal density calculator is used for calculating densities at 0°C and one-atmosphere pressure. The CGS and SI units of density are g/cm3 and kg/m3 and dimension [ML−3].
The reciprocal of the density is called specific volume, a term that is sometimes used widely in thermodynamics. Therefore, specific volume can be defined as the volume per unit mass of a substance.
Density of Solids and Liquids
Generally, solid materials are much more danced compared to liquid forms but the solid form of water (ice) is less danced than liquid water. Hence solid ice is lighter than water and floats easily in water.
The densities of a solids and liquids material varies with temperature and pressure and the variation is typically small for solids and liquids but much greater for gases. Commonly, the density of solid or liquid substances decreases when temperature increases. It is due to the rise in temperature, the volume of such substances increses.
Density of Gases
The densities of gases are minimum at a specific temperature and pressure. This is due to the fact that a given volume of gas is much lighter compared to that of a solid or a liquid.
The ideal gas law formula is used to calculate the molar mass and density of ideal gases. It is approximately obeyed under normal temperature and pressure. Therefore, the density measured by the ideal gas equation is not an accurate one.
Density Examples
Solid have much dense materials as compared to their liquids or gas forms. Sugar, sand, rocks, stones, and metals like iron, copper, aluminum, gold, and silver are common examples of solid materials which are much dense materials as compared to their liquid forms. The dense materials are most likely to be heavy or hard in nature.
In general, liquid materials are less dense than solid materials but more dense than gaseous materials. This is due to the fact that solid materials have densely packed particles compared to liquid materials where particles can slide around one another. In a gas state, the built particles can be free to move from one place to another.
Water, milk, juice, oil, kerosene, petrol, alcohol, and benzene are common examples of liquid substances that we use widely in our lives. The liquid forms of these substances are less denser than their solid form but liquid water is much denser than solid water (ice).
Some density examples of common elements and substances at O °C temperature and 1 atm pressure are given below in the table,
| Material | Density (kg/m3) |
| Hydrogen | 0.0898 |
| Helium | 0.179 |
| Air | 1.23 |
| Carbon dioxide | 2 |
| Lithium | 535 |
| Potassium | 860 |
| Ice | 916.7 |
| Wax | 960 |
| Sodium | 970 |
| Glass | 2,500 |
| Diamond | 3,500 |
| Stainless steel | 7,800 |
| Iron | 7,870 |
| Brass | 8,530 |
| Copper | 8,940 |
| Silver | 10,500 |
| Lead | 11,340 |
| Gold | 19,320 |
| Platinum | 21,450 |
Density Measurement
The densities of solids, liquids, and gases are the measurement of mass per unit volume at a given temperature and pressure. The standard or normal density of solids, liquids, and gases can be measured at 0°C temperature and one-atmosphere pressure.
Various types of techniques can be used for measuring the density of a specific material. Therefore, it is necessary to understand the type of density that we measured and the type of material that we take for measuring.
The density of homogeneous materials at all points equals and it can be measured by dividing the total volume by the total mass of the materials. For heterogeneous materials, it can vary from one region to another. Therefore, various small volumes around various locations can be used to calculate the density of the said material.
In gases, we also used relative density for measurement. It is the ratio of masses of an equal volume of gas and oxygen. The densities of gases is also related to Graham’s law of diffusion or effusion.
Density Formula for Gas Molecules
The ideal gas equation for n mole gases,
PV = nRT
From the above equation,
P = nRT/V = gRT/MV = ρRT/M
where ρ = symbol of the density
M = molar mass of gases
The molar mass of the gas can be experimentally determined by using this expression.
Limiting Densities
Such density definition or calculation from the above gas equation measured only an approximate and not an accurate one for learning chemistry or chemical science. But the above equation is accurately obeyed at very low pressure at P→0. Therefore, the equation is represented as,
M = (ρ/P)P→0 × RT
where (ρ/P)P→0 = limiting the density of a gas
Pressure vs Density Graph for Ideal Gas
The pressure versus limiting density graph of an ideal gas is shown below the figure,
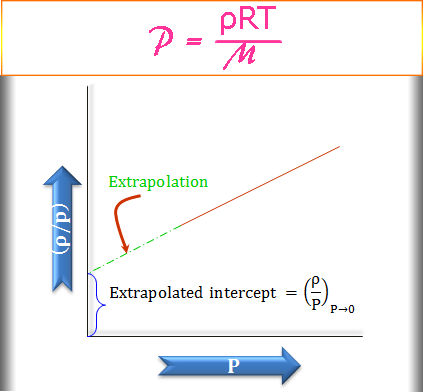
The direct use of the limiting density formula causes some difficulty since, at P→0, ρ→0 and not possible to determine experimentally. Therefore, the above graphical measurement has taken advantage of the calculation of molar mass.
Problem: At 0° temperature, the density of gaseous non-metallic oxide at 2 atm pressure is the same as that of oxygen at 5 atm. Find the molecular weight of the nonmetallic substance.
Solution: From the density formula,
M = MO2 × (PO2/Pnon-mettalic)
= 32 × (5/2)
= 80 g/mol
What is Vapour Density?
Vapour density of a substance is defined as the ratio of the density of the gaseous substance and hydrogen under the same temperature and pressure.
It is the quantity having no unit or dimensions and is represented by the formula,
D0 = M0/2
where M0 = formula molecular weight of the gases
Abnormal Densities
Many chemical substances, like ammonium chloride, phosphorus pentachloride, hydrogen peroxide, iodine, etc have calculated vapour densities less than the theoretical measurement. Only at a high temperature, it obeys the formula D0≈D0/2. This phenomenon is called abnormal densities.
The cause of this phenomenon due to the thermal bond dissociation of the above chemical substances.
NH4Cl → NH3 + HCl
For the above chemical equation, one mole of ammonium chloride dissociates to form one mole of ammonia and one mole of hydrogen chloride vapour. Therefore, the volume of the vapour has doubled at the same temperature and pressure. Hence the density of ammonium chloride will be halved.
Similarly, phosphorus pentachloride (PCl5), dinitrogen tetraoxide (N2O4), and iodine (I2) dissociate to form respective vapour molecules. The dissociation of such substances is represented by,
PCl5 → PCl3 + Cl2
N2O4 → 2NO2
I2 → 2I
The volume of the vapour of such substances increses at the same temperature and pressure. Therefore, the density of such substances is lower than the theoretical measurement.
Formula for Calculating Abnormal Densities
At constant pressure due to the dissociation of the chemical bond, the volume of the gases increases with the increase of the mole number. Since mass remains the same and D0 decreases.
The extent or fraction of the total number of molecules that suffer dissociation calculates the degree of dissociation. Let us take one molecule of substance A splits up into n molecules of B by the specific heat,
A → nB
At equilibrium for each gram mole of A will be (1 − α) gram moles of undissociated A and nα gram moles of B.
So the total number of gram moles of gas present
= (1 − α) + nα
= 1 + (n − 1)α
When V = volume occupied per unit volume of gas or vapour and D0 defines the density measurement absence of any dissociation. If D denotes the observed density when actual dissociation occurred and the total weight of the gas = W.
W = DOV and W = D×V[1 + (n − 1)α]
Therefore, D0/D = 1 + (n − 1)α
The above expression shows that, at high temperature, α = 1 (complete bond dissociation) and for NH4Cl, and PCl5, n=2. Thus, the density, D = D0/2. Therefore, the above formula is used to calculate the vapour densities of various dissociated substances.
Frequently Asked Questions – FAQs
What is density?
Density is the measurement of a material that identifies how tightly the smallest units of such material are packed together.
It can be derived by the symbol D or ρ and the formula
ρ = m/V
where ρ is the density, m is the mass of the material and V is the volume of the material
Why density is important?
Density is an important property of a material that can be easily measured by various techniques. It is widely used to identify pure substances and characterize the composition of many kinds of mixtures. It also determines whether or not an object will float on water. Density is the basis for gold mining, blood separation, DNA extraction, etc.