Van der Waals Equation of State
Van der Waals equation of state is given by modifying the ideal gas law in 1873. He put the reasons for the deviations of the real gases from ideal behavior. Van der Waals introduced the size effect and the intermolecular attraction effect of the real gases. These two effects or factors in the Van der Waals equation arose because he considered the size and intermolecular attraction among the gas molecules. These two effects in learning chemistry are discussed under volume correction and pressure correction of the ideal gas equation. Van der Waals proposed that the two postulates used in the kinetic theory of gas molecules are not applicable to real gases. These two assumptions are the gas molecules are point masses or practically they have no volumes and there is no intermolecular attraction in the gas molecules.

Liquefaction of Gases
The molecule occupies a certain volume as seen from the fact that gases can be liquified or solidified at low temperatures and high pressure. On decreasing pressure, the thermal energy or specific heat of gas molecules decreases which favors liquefaction, diffusion, or solidification.
In crystalline solids, the atoms, ions, or molecules are considerably resistant to any further attempt of compression but gas molecules are compressible.
Van der Waals was the first to introduce the mathematical calculation or correction formula of the ideal gas equation,
PiVi = nRT
Volume Correction Factor
In learning chemistry or physics, real gas molecules are assumed to be a hard rigid sphere. Therefore, the available space for the free movement of the molecules becomes less than the original molar volume.
The available space for the free movement of 1-mole real gas molecules,
Vi = V − b
Where Vi and V = molar volume of ideal and real gases respectively
b = volume correction factor
Molecular Diameter of Gases
Let us take a gas molecule with radius r and diameter σ = 2r. When two molecules encounter each other the distance between the centers of the two gas molecules would be the diameter (σ ) of the molecule. Therefore, the space indicated by the dashed circle below the picture will be unavailable space for the pair of molecules.

The solution of the volume correction factor (b) helps for the calculation of the diameter or radius of the gas molecule. Therefore, after this volume correction formula of gas, the ideal gas equation is written as,
Pi (V − b) = RT
Pressure Correction Formula
The pressure of the gas is developed due to the wall collision of the gas molecules. However, due to intermolecular attraction, the colliding molecules will experience an inward pull. Therefore, the pressures exerted by the molecules in real gases will be less than the ideal gases.
The ideal gases have no intermolecular attraction.
∴ Pideal > Preal
or, Pideal = Preal + Pa
where Pa = pressure correcting term for real gases
The higher the intermolecular attraction in the gas molecules greater the magnitude of the pressure correction term. Therefore, the pressure correction term depends on the frequency of molecular collisions.
The average pressure exerted by the molecules decreased by Pa, which is proportional to the square of the density of gas molecules.
Therefore, Pa ∝ 1/V2, since density ∝ 1/V
∴ Pa = a/V2
where a = Van der Waals constant for gases
Van der Waals Equation Derivation
Using pressure and volume corrections factor formula, Van der Waals equation of state for 1 mole real gas,
(P + a/V2)(V − b) = RT
For n moles real gases, the volume has to change because the volume is a thermodynamics extensive property in this equation. Therefore, the Van der Waals equation of state for n mole real gases,
(P + an2/V2)(V − nb) = nRT
Important Points
Gases where a = 0 but b ≠ 0
For Van der Waals gases which have no intermolecular attraction (a = 0) but size effect considered (b ≠ 0).
In such cases,
Preal > Preal = nRT/(V − nb)
Since Pideal = nRT/V only
It means that the molecular size effect of the molecules (repulsive interaction) creates higher pressure than that observed from the ideal gas law and the mass or volume of gas molecules is negligible.
Gases where b = 0 but a ≠ 0
For the real gases which have attractive force (a ≠ 0) but size effect not considered (b = 0).
In such cases,
Preal < Preal
Therefore, the intermolecular attraction reduces the pressure of real gases.
Units of Van der Waals Constant a and b
Van der Waals equation of state is used for the calculation of units and dimensions of constants a and b.
From the Van der Waals equation for n-mole real gases,
Pa = an2/V2
where Pa = unit of internal pressure
Therefore, the unit of Van der Waals constant,
a = atm lit2 mol−2
Again nb = unit of volume, hence unit of Van der Waals constant,
b = lit mol−1
In the SI system,
The unit of a = (N m−2) m6 mol−2
= N m4 mol−2
The unit of VDW constant b = m3 mol−1
The dimensions of the Van der Waals constant,
a = [M L5 T−2 mol−2]
b = [L3 mol−1]
Significance of Van der Waals Constant
Significance of Pressure Correction Factor
The pressure correction factor (a) originates from the intermolecular attraction and Pa = an2/V2. Therefore, the internal pressure of the gas can be measured by the pressure correction factor.
The higher the value of the pressure correction factor greater the intermolecular attraction and the more easily the gas liquefied.
Van der Waals constant (a) for greenhouse gas carbon dioxide gas = 3.95 but hydrogen gas = 0.22.
Significance of Volume Correction Factor
Another constant volume correction factor (b) measures the molecular size and also repulsive forces.
The greater, the value of b larger the size of the gas molecule. Van der Waals constant b for carbon dioxide = 0.04 but hydrogen = 0.02.
Compressibility Factor for Real Gas
Van der Waals equation is used for the calculation of Boyle temperature, and critical temperature. It also explains the compressibility factor and Amagat curves for n-mole real gases.
Mathematical calculation of Boyle temperature for real gases,
TB = a/Rb
The compressibility factor is the function of temperature and pressure only.
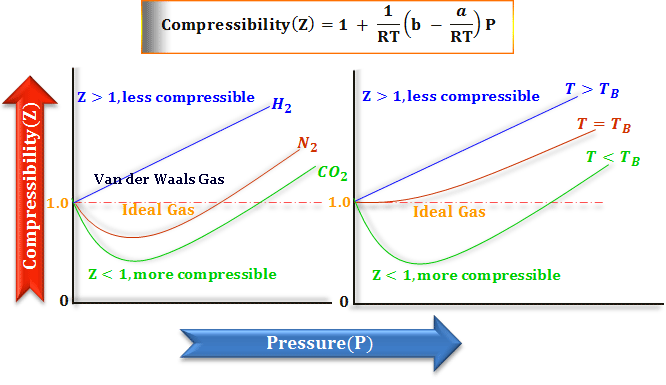
- When b > a/RT, the initial slope is positive and the size effect or factor (b) dominates the base properties of the gas.
- However, b < a/RT, the initial slope is negative and the effect of attractive forces (a) dominates.
The Van der Waals equation balances both size effect and intermolecular forces in the positive and negative plot of compressibility vs pressure.
Van der Waals Gases
From the above slope, we can say that at 0°C, the effect of attractive forces dominated (carbon dioxide, nitrogen, and hydrocarbons like methane, ethane, acetylene), while the molecular size effect dominates for the behavior of hydrogen gas.
The unit value of the Van der Waals constant for hydrogen, helium, nitrogen, etc for studying chemistry or physics is extremely small as these gases are difficult to liquefy.