Home Chemistry Gas Laws Ideal and Real Gases

Ideal and Real Gases

Ideal gas and real gas

Ideal gas and real gas molecule can be compared by the ideal gas law or equation for different types of gases. The gases which obey ideal gas law under all conditions of temperature and pressure are called ideal gases but which does not obey ideal gas law under all condition of temperature and pressure are called real gases. Different Gas Law formulas can be used to compare physical properties like density, molecular weight, diffusion, thermal energy, and compressibility for ideal and real gases in physics or physical chemistry.

Difference between ideal gas and real gas by compressibility factor formula

Why is an ideal gas considered hypothetical?

An ideal gas is a really hypothetical one because under the maintained temperature and pressure it transformed into the liquid state. But we assumed that ideal or perfect gases molecule has no intermolecular attraction.

Properties of ideal gases

  • An ideal gas can not be liquefied because the gaseous molecule has no intermolecular attraction.
  • The coefficient of thermal expansion (É‘) depends on the temperature of the gases and does not depends on nature.
  • The coefficient of compressibility (β) similarly depends on the pressure and will be the same for all gases.
  • When pressure is plotted against volume at a constant temperature a rectangular hyperbola curve is obtained according to Boyle’s law.
  • When PV is plotted against pressure at a constant temperature a straight line parallel plot is obtained.
  • If the ideal gas passes through a porous plug from higher pressure to lower pressure within the insulated enclosure, there will be no change in the specific heat or temperature. This confirms that the ideal gases have no inter-molecular attraction.

Properties of real gases

  • Real gas could be liquefied because the gaseous molecule has the property of intermolecular attraction which helps to coalesce the molecule.
  • The coefficient of thermal expansion (α) depends on the nature of the gaseous molecule.
  • The coefficient of compressibility (β) was also found to depend on the nature of the gases.
  • When pressure is plotted against volume a rectangular hyperbola curve is obtained only at a high temperature above the critical temperature.
  • But a temperature below the critical temperature (TC), the molecule can be liquefied after certain pressure depending on temperature.
  • Liquid and gas can be indistinguishable properties in the critical point of the gases. When PV is plotted against pressure for real or Van der Waals gases, the Amagat curve is obtained.
  • Real gases pass through porous plugs from higher pressure to lower pressure within the insulated enclosure, there occurs a change in temperature.
  • Real gases have inter-molecular attraction and when expanded, the molecules have to spend more kinetic energy to overcome inter-molecular attraction. Therefore, the temperature drops down.

Coefficient of thermal expansion

In thermodynamics, the coefficient of thermal expansion and compressibility can be defined as,

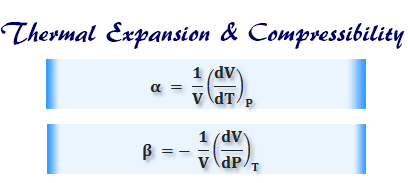
Compare thermal expansion and compressibility of ideal gases

For one mole ideal gases,
PV = RT
∴ α = R/PV = 1/T

Therefore, the thermal expansion will be independent of nature and will be a function of temperature only.

For example, the coefficient of thermal expansion for hydrogen and carbon dioxide gases is 2.78 × 10−7 and 3.49 × 10−7 respectively at 0°C and 500 atm pressure. For real gases, the coefficient of thermal expansion depends on the nature of the gases.

Coefficient of compressibility

Coefficient of compressibility for ideal gases,
β = RT/P2V = 1/P

Therefore, β should be a function of pressure only and the same for all gases. But experimentally the coefficient of compressibility has been found to be individual property.

PV vs P graph for real gas

When PV is plotted against P for real gases following plots are obtained. It is called Amagat curves.

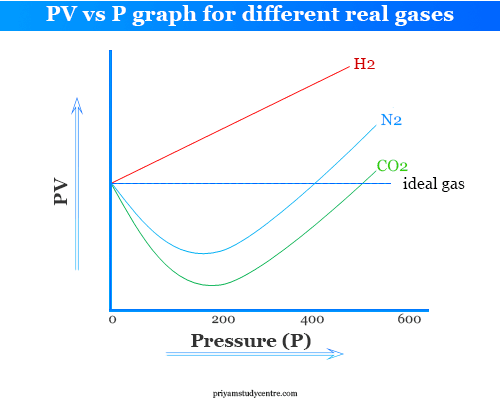
PV vs P graph for different real gases like hydrogen, nitrogen and carbon dioxide

The value of PV decreases attains minimum and then increases with the increased pressure.

  • Only hydrogen and helium baffled this compression trend and the curve rise with increased pressure from the very beginning.
  • Carbon dioxide can be easily liquefied and PV dips sharply below the ideal gas line in the low-pressure region.

At very low pressure (below 1 atmosphere), the plot PV-P is linear but different for different gases.

In the case of carbon dioxide, oxygen, hydrocarbon (methane, ethylene), and nitrogen, the PV values first diminish and reach the minimum, then increases.

Boyle temperature

Every gas has a characteristic temperature where the curve PV-P runs parallel to the P-axis from zero pressure to moderate value of pressure. It means, at this temperature, the value of PV is constant for an appreciable range of pressure. This temperature is called Boyles temperature or Boyle point of the gas.

Mathematically TB can be defined as,
TB = d(PV)/dT = 0, when P → 0

Gases Boyles temperature
hydrogen (H2) − 156 °C
helium (He) − 249 °C
nitrogen (N2) 59 °C
methane (CH4) 224 °C
ammonia (NH3) 587 °C

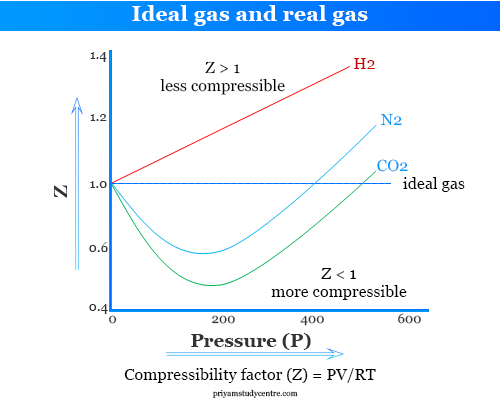
Compressibility factor formula

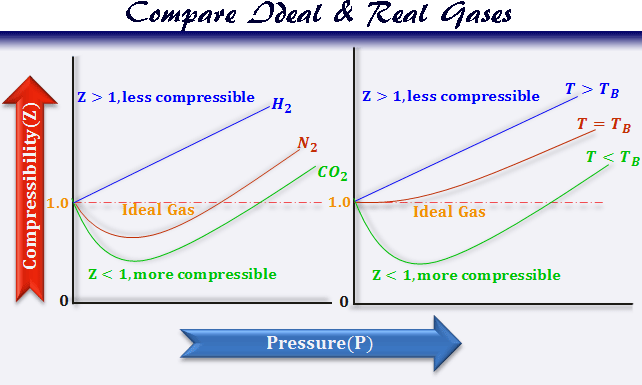
Compare the property of ideal gases and real gas molecule

An important single parameter called the compressibility factor is used to compare the extent of deviation of the real gases from ideal behavior in learning chemistry or physics.

The compressibility factor can be defined as,
Z = PV/RT
where V = the molar volume

  • When Z=1, there is no deviation from the ideal behavior.
  • When Z ≠ 1, the departure of the unit value of Z is a measure of the extent of non-ideality.
  • Z < 1, the gas is more compressible than ideal gases.
  • When Z > 1, real gases are less compressible than ideal gases.

RELATED ARTICLESALL ARTICLES