Bond Moment and Dipole Moment
Dipole moment formula in chemistry is used to find out or calculate the net bond moment and polar character or polarity of the molecules such as water, ammonia, methane, carbon dioxide, carbon monoxide, etc. The product of charge and distance of separation of atoms in chemical bond uses for calculation of the term dipole moment of molecules. When +q amount of positive charge is separated by −q amount of negative charge by the bond distance l, then dipole moment (μ) of polar molecule = q × l. Therefore, perfectly non-polar molecules hydrogen, oxygen, and nitrogen have zero dipole moment. The polar molecules like water, ammonia, and methane have positive values. The dipole moment is a tool used to calculate or find out the percentage ionic character, electric polarization, and net residual charge on the atoms of the molecules.
Examples of Polar Molecules
When the center of gravity of the positive charge does not coincide with the center of gravity of the negative charge, polarity arises in the molecules. These molecules are called polar molecules. Hydrogen chloride, water, methyl chloride, and benzyl chloride are examples of polar molecules.
Unit of Dipole Moment
In the CGS system, the charge is expressed in esu and bond length in cm. Therefore, the unit of dipole moment is esu cm. The charge is of the order of 10−10 esu and the distance of separation is the order of 10−8 cm. Hence the order of μ is 10−18 esu cm. This magnitude is called 1 Debye.
∴ 1 Debye = 10−18 esu cm
In the SI system, the charge is expressed in coulomb and the length is meter. Hence the unit of dipole moment in the SI system is the coulomb meter.
Debye to Coulomb Meter
In the CGS system,
μ = 4.8 × 10−10 × 10−8 esu cm
= 4.8 Debye
In the SI system,
μ = 1.6 × 10−19 × 10−10 coulomb m
= 16 × 10−30 coulomb m
∴ 4.8 Debye = 16 × 10−30 coulomb m.
Form the above formula,
1 Debye = 3.336 × 10−30 coulomb m
Dipole Moment Formula
It is used for the calculation of the percentage ionic character, bond angle, electric polarization, and residual charge on the atoms in the molecules. It also helps to determine the size or shape of molecules and the arrangements of chemical bonds in the molecules.
Dipole Moment and Percentage Ionic Character
Dipole moment data is used to calculate the percentage ionic character of covalent or ionic heteronuclear diatomic molecules. Let us consider a molecule AB having the observed dipole moment = μobs and the bond length l cm.
- If the shared pair lies at the midpoint of the atoms, the bond would be a purely covalent bond, and the percentage ionic character is zero.
- But if the bond is 100 percent ionic and B is more electronegative than A. Therefore, A carries a unit positive charge, and B carries a unit negative charge.
Percentage Ionic Character Formula
In that case, the μ of AB would be, μionic = e × l = 4.8 × 10−18 esu cm. But the μ of AB is neither zero nor μionic.

Calculate the Percentage ionic character of HCl
If we consider HCl as a purely ionic compound the charge on hydrogen and chlorine = 4.8 × 10−10 esu and bond length = 1.27 × 10−8 cm.
The μionic of HCl,
μionic = e × l
= 4.8 × 10−10 × 1.27 × 10−8 esu cm
The calculated or observed dipole moment,
μobs = 1.03 Debye
= 1.03 × 10−18 esu cm
The percentage ionic character of HCl,
= (µobs/µionic) × 100
= (1.03 × 10−18/4.8 × 10−10 × 1.27 × 10−8) × 100
∴ % of ionic character in HCl = 16.89
Electric Polarization Formula
In learning chemistry, the induced electric polarization formula is used to calculate the radius of the molecules. The induced electric polarization formula of the molecules is,
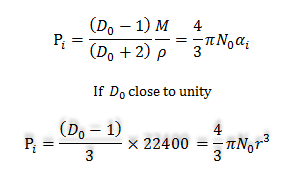
At standard temperature and pressure (STP),
M/ρ = molar volume or density
= 22400cc/mole
For spherical molecules,
αi= r3
Therefore, r3 = (22400/4πN0)(D0 −1)
= 2.94 × 10−21 (D0 −1)
Therefore, with the known value of capacitance, we can easily determine the radius of the molecule.
Dipole Moment Examples
The dipole moment is used to define the structure, bond angle, bond energy, and polarity of different molecules in chemistry. Mono-atomic noble gases and benzene are non-polar because the charge of the constituent atom is distributed symmetrically.
Homonuclear Diatomic Molecules
Homonuclear diatomic molecules like nitrogen, oxygen, and chlorine have zero net bond moment due to the symmetrical charge distributions and similar electronegativity and ionization energy.
Heteronuclear Diatomic Molecules
Hydrogen bromide and hydrogen iodide have non-zero dipole moments indicating the unsymmetrical charge distribution between two bonding atoms in the molecules.
Due to the difference in electronegativity of the constituent atoms in heteronuclear diatomic molecules are always polar. Hence the electron pair is not equally shared in the hydridized orbital and shifted to the more electronegative atom. Therefore, μHCl = 1.03 Debye, μHBr = 0.79 Debye, μHI = 0.38 Debye, μHF = 2.00 Debye.
Dipole Moment of CO
The electronegativity difference between carbon and oxygen in CO is very large but the net dipole moment of carbon monoxide is very low. This suggested that the charge density in the oxygen atom somehow back-donated to the carbon atom. Hence CO formed a coordinate covalent bond directed towards the carbon atom to decrease polarity.
How to Calculate Dipole Moment?
Carbon dioxide (CO2), beryllium chloride (BeCl2), and stannous chloride (SnCl2) have zero bond moments indicating that the molecules have symmetrical linear structures. In CO2, one carbon-oxygen bond cancels the bond moment of the other carbon-oxygen bond.
Dipole Moment Calculation
The electric moment associated with the bond arising from the difference in electronegativity is called the bond moment (m). In a molecule, the vectorial addition of the bond moments is used for the calculation of the μ.
Hence, μ2 = m12 + m22 + 2m1m2Cosθ
Where m1 and m2 are the bond moments projecting at the angle of θ. Bond moment and net dipole moment calculation help to find the bond angle of CO2, H2O, H2S, SO2, etc.
For CO2, µ = 0 and m1 = m2 = m
Therefore, 0 = 2m2(1 + cosθ)
or θ = 180°
For H2O, H2S, and SO2 molecules, θ < 180°. Therefore, these molecules are non-polar because they have non-linear structures.
| Molecule | Molecular Formula | Dipole moment (Debye) | Bond angle |
| Carbon dioxide | CO2 | 0 | 180° |
| Water | H2O | 1.84 | 105° |
| Hydrogen sulfide | H2S | 0.94 | 97° |
| Beryllium chloride | BeCl2 | 0 | 180° |
| Sulfur dioxide | SO2 | 1.61 | 119° |
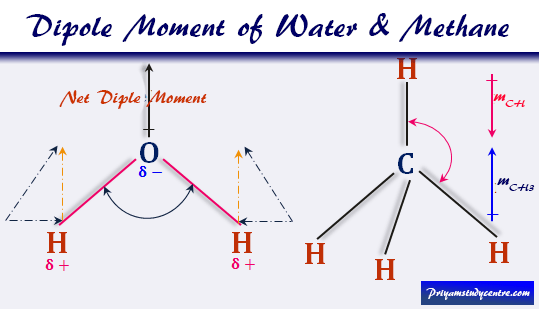
Dipole Moment of Water
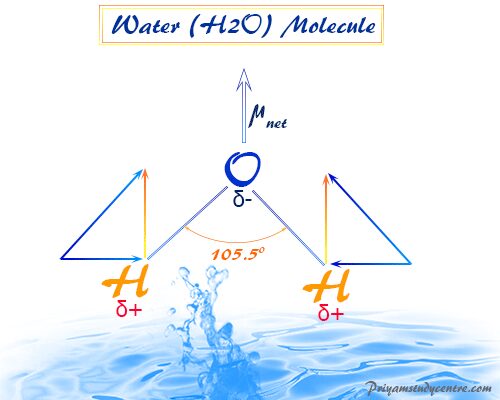
For water (H2O), μwater = 1.84 Debye and bond moment (mOH) = 1.60 Debye.
Therefore, (1.84)2 = 2(1.60)2(1 + cosθ)
From the above formula θ = 105°. Therefore, the contribution of non-bonding electrons toward the total dipole moment is included within the bond moment of water.
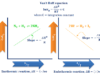
Dipole Moment of BF3 and BCl3
Boron trichloride (BCl3), and boron trifluoride (BF3) are the tetratomic compounds having net dipole moment zero, indicating that they have a regular planar structure.
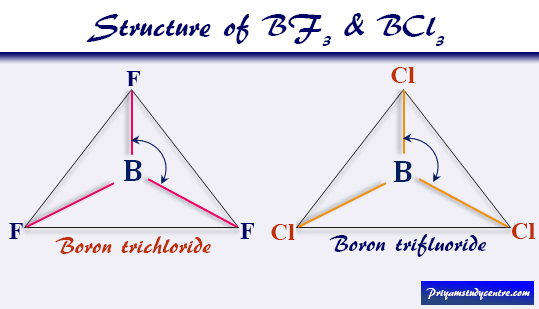
From the above picture, three halogen atoms are on a plane at the corner of the equilateral triangle, and a boron atom at the intersection of the medians. Therefore, the μnet of the BCl3 and BF3 is zero.
Dipole Moment of NH3 and PH3
Other types of the molecule such as ammonia (NH3) and phosphine (PH3) are polar, where μ≠0 indicates that the molecule has a pyramidal structure. Hence three hydrogen atoms are on the plane and nitrogen or phosphorus atoms are at the apex of the pyramid in the NH3 or PH3 molecule.
Dipole Moment of NF3
NF3 shows a very small bond moment although there is a great difference in electronegativity and electron affinity between nitrogen and fluorine atoms and a similar structure of NH3.
- The low value of µ in NF3 is explained by the fact that the resultant bond moment of the three nitrogen-fluorine bonds is acting in the opposite direction to that of the lone pair placed at the nitrogen atom.
- But in NH3, the resultant bond moment is acting in the same direction as that of the lone pair electrons.
How to Find Net Dipole Moment?
Methane (CH4), carbon tetrachloride (CCl4), and platinum chloride (PtCl4) are examples of penta atomic molecules having zero net dipole moment. This suggests that they are either regular tetrahedral or square planer structures. However, the polar molecules of this type have pyramidal structures.
Dipole Moment of Methane
For the calculation of the μ of methane, let us discuss the structure of methane. In methane molecules, the valence shell electronic configuration of central carbon atom 2s2 2p2. Hence the carbon atom in methane sp3 hybridized to form a regular tetrahedral structure with the angle of each H-C-H = 109°28ˊ.
The electric moment associated with a group is called a group moment. It depends on the arrangement of the bonds in the groups. The difference in the electronegativity of the constituent atoms forming the bonds in the group.
It can be shown that the group moment of the methyl group (mCH3) is identical to the bond moment of a carbon hydrogen bonding (mCH).
From the structure and bond moment,
mCH3 = 3 mCH × Cos(180° -109°28՛)
= 3 mCH Cos 70°32՛
= 3 mCH × (1/3)
Therefore, mCH3 = mCH
Therefore, two bond moments cancel each other to show zero net bond moment in the methane (CH4) molecule.
The net moment can be also calculated by another method,
µmethane = mCH (1 + 3 Cos 109°28՛)
= 0
How to Find the Dipole Moment of a Molecule?
Dipole moment of CCl4
By a similar calculation, it can be shown that mCCl3 = mCCl = m in chloroform (CCl4). Therefore, the net dipole moment for the CCl4 molecule can be calculated by the following formula:
μchloroform = 2m2(1 + Cosθ)
= 0
Here, Cosθ = Cos180° = −1
Dipole Moment of Chloromethane
The molecular formula of chloromethane is CH3Cl. The measurement of the polarity of the chemical bond in a CH3Cl is used for the calculation of μ.
We know, μ2 = m12 + m22 + 2 m1m2 Cosθ
For dichloromethane (CH3Cl), θ = 0° hence Cosθ = 1.
∴ μchlorometane = (m1 + m2)
= (1.5 D + 0.4 D)
= 1.9 D
Dipole Moment of CHCl3
Similarly, for trichloromethane (CHCl3), θ = 0° hence Cosθ = 1.
∴ μCHCl3 = (m1 + m2)
= (1.5 D + 0.4 D)
= 1.9 D
Zero Dipole Moment Examples
A similar calculation is done for μ of hydrocarbons like ethylene and acetylene in organic chemistry. The hydrocarbons ethylene and acetylene have zero dipole moments because the individual bond dipoles cancel each other which results in zero net dipole moments.
The bond moment of alcohol is also calculated by the dipole moment formula. The bond moment of mOH = 1.6, mC-O = 0.7, mCH3 = mCH = 0.4 Debye. Therefore, the resultant dipole moment of methyl alcohol = 1.56 while the observed value = 1.65 debye.