What are gases?
Gases are the state of matter in which molecules are far apart from each other and characterized by a lack of definite volume and density. Boyle’s law, Charles law, Avogadro law, Gay Lussac law, ideal gas law, and Graham’s law provide the relation between mass, pressure, volume, temperature, and density of ideal gas molecules.
Careful experiments show that the ideal gas laws are only approximately obeyed by different gases. The gases which do not obey these laws are called real gases.
The ideal gas equation can be used to distinguish between ideal gas and real gas. The gas which obeys this equation is called ideal gas and which does not obey this equation is called real gas. Van der Waals equation is used to derive the properties of real gases.
Properties of gases
- In the gaseous state, the matter has the property of filling completely to any available space of uniform density.
- The low density, high compressibility are also important properties of the gases.
- The gases are formed when thermal energy is much greater than the force of attraction.
- Among crystalline solid, liquid, and gaseous states of aggregation, the gases are allowed for the comparative study between mass, pressure, volume, and temperature, density, heat capacity, etc.
Formula of gases
The physical properties of gases are very simple and identical for all gases. These properties of different gases are evident from the fact that all gases generally obey some simple or common gas formula or relation. These are called gas laws.
In learning chemistry or physics, Boyle’s, Charles, Avogadro, Gay Lussac, and Graham’s laws are common laws that derive the formula of ideal gases. After knowing these experimental ideal gas laws, a theoretical model-based structure of gases was developed by kinetic theory gas equation.
What is Boyle’s Law?
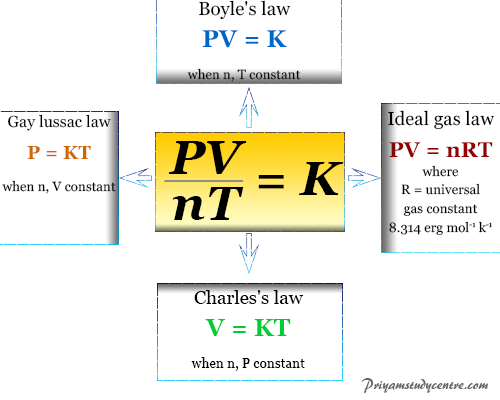
Boyle’s law states, at a constant temperature, the volume of a definite mass of a gas is inversely proportional to its pressure. Therefore, the volume of a given quantity of gases, at constant temperature equilibrium with the pressure of gases.
At constant temperature and 1 atm pressure, a cylinder contains 10 ml of methane or hydrogen gas. If the pressure increases to 2 atm then according to Boyle’s law volume decreases to 5 ml.
Boyle’s Law formula
According to the definition of Boyle’s law
V ∝ 1/P, when temperature (T) is constant
or PV = K = constant for a gas.
The value of the gas constant depends on the nature and mass of the gas molecules. For a given mass of gas, if the volume V1 at pressure P1 and volume V2 at pressure P2. Therefore, according to Boyle’s Law,
P1V1 = P2V2.
Graphical representation of Boyle’s Law
The relation between pressure and volume of gas can be represented by an arm of a rectangular hyperbola graph given below the picture,
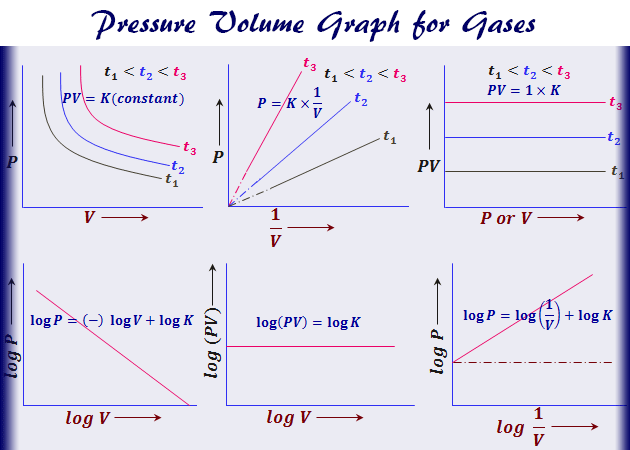
- The value of gas constant changes with temperature. There will be a separate two-dimension curve for each fixed temperature. When these curves are plotted at different fixed temperatures called isotherms.
- At constant temperature, a given mass of gas is the product of pressure and volume. If the product of pressure and volume of gas represents on the y-axis and pressure represents the x-axis a straight-line graph is obtained parallel to the x-axis.
Pressure and density relationship
Let at a constant temperature, M mass of gas has pressure P1 at volume V2 and pressure P2 at volume V2.
According to Boyle’s law,
P1V1 = P2V2
or, P1/P2 = V2/V1.
Let the density of the gas D1 at pressure P1 and D2 at pressure P2.
Therefore, D1 = M/V1
or, V1 = M/D1
D2 = M/V2
Putting the values on Boyle’s law formula,
P1/P2 = V2/V1 = D1/D2
or, P ∝ D
Therefore, at a constant temperature, the density of a definite mass of gases is proportional to its pressure.
What is Charles Law?
Charles law made measurement of the volume of a fixed mass of a gas at various temperatures under the condition of constant pressure. Charles law states that at constant pressure, the volume of a given mass of a gas is a linear function of temperature.
Charles Law mathematical formula
At constant pressure, each degree rise in temperature of a definite mass of gas expands 1/273.5 of its volume at 0⁰C. Let V0 = volume at 0⁰C. 1⁰C rise of temperature the volume of the gas rise V0/273.5 ml.
It is convenient to use the absolute temperature scale on which temperature is measured in Kelvin. Hence the reading on this scale was obtained by adding 273 to the Celsius value. Therefore, TK = 273 + t°C.
The Charles law is represented as
Vt = (V0 × T)/273 = (V0/273) × T.
Since V0 = initial volume = constant at a given pressure. Hence the above relation is expressed as,
Vt = K2 T, where K2 = constant
According to this gas formula, Charles Law states as, at constant pressure, the volume of a given mass of gas is directly proportional to its kelvin temperature.
Graphical representation of Charles Law
A typical property of the volume of gases with a change in its kelvin temperature is a straight-line isobar graph obtained. Thus the general term isobar, which means constant pressure assigned to these plots.
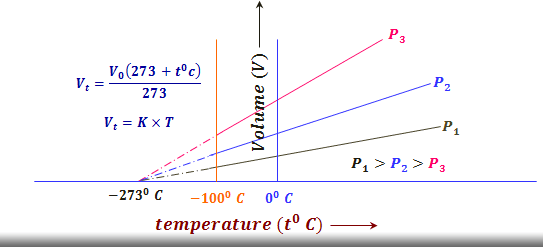
What is absolute zero temperature?
Since volume is directly proportional to its kelvin temperature. Thus the volume is theoretically zero at zero kelvin or – 273 °C. This is hypothetical because the molecule of our environment has physical properties to form liquid and then solid before this low temperature of the gas is reached.
In reality, no substance exists in gases at this temperature near kelvin zero. For the liquefaction of real gases, we must maintain critical temperature.
Density and temperature relationship
Let at constant pressure, for M mass of gas has volume V1 at temperature T1 and volume V2 at temperature T2. According to Charles law,
V1/V2 = T1/T2
Again let the density D1 and D2 at V2 and V1 respectively.
Therefore, T1/T2 = V1/V2 = D2/D1
or, D ∝ 1/T
According to the above formula, at constant pressure, the density of a given mass of gases is inversely proportional to its temperature.
What is Avogadro’s Law?
The volume of gas depends not only on the quantity of the gas but also on its pressure and its temperature. It is common knowledge that at any given temperature and pressure, the volume of a gas will be directly proportional to the quantity.
Therefore, V ∝ n
when pressure (P) and temperature (T) are constant.
The quantity n is expressed in g moles. For example, 32 gm oxygen gas equal to 1 g moles oxygen.
In 1811, Avogadro discovered the Law of gases is called the Avogadro law. According to the law, measured at a common temperature and pressure, the volume of the same number of g moles of different numbers of gases would be the same.
In other words, at common temperature and pressure, 1g moles (28 gm) nitrogen and 1 gm moles (32 gm) oxygen occupy the same volume.
Combined gas law formula
Charles law, V ∝ 1/P when T constant, and Boyle’s law, V ∝ T when P constant in chemistry or physics.
When all the variables are taken into account the variation rule states,
PV = KT
All gases have properties to obey the gas laws formula under all conditions of temperature and pressure. For real gases, the Van der Waals equation is needed to explain the properties of gases.