Kinetic Molecular Theory of Gases
Kinetic molecular theory of gases and the kinetic gas equation was first developed by Bernoulli in 1738 to derive the molecular properties of gas molecules on the basis of the ideal gas law and mechanical energy formula. For the study of physics and chemistry, the kinetic theory of gases consists of many postulates or assumptions. In the nineteenth century, the efforts of Joule, Kronig, Clausius, Boltzmann, and Maxwell, gives the postulates or assumptions of the kinetic theory of gases and kinetic gas equation or formula on the basis of root mean square velocity (RMS) and momentum of the gas molecule. Molecules in the gaseous state of matter move generally at very large speeds and the forces of attraction are not sufficient to bind the molecules in one place.
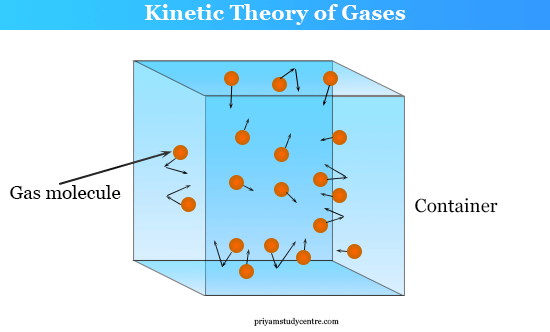
Solid Liquid and Gas Molecules
- Solid Molecules: Solid molecules or particles are held very closely together and are entirely devoid of any translatory motion. When a specific heat is supplied to a crystalline solid, it takes the form of vibrational motion with the rise of temperature.
- Liquid Molecules: Further increases the thermal energy, the vibrational motion rises, and the molecules break down to transform into a liquid state like ice to water.
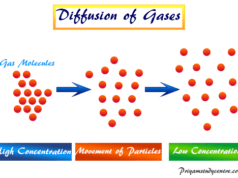
- Gas Molecules: When the thermal energy is much greater than the forces of attraction, then we have a gaseous state of matter. The gas molecules move randomly and collide with the walls of the container (wall collision) and with themselves (intermolecular collision). These collisions are perfectly elastic. Therefore, there occurs conservation of energy because of no loss of kinetic energy or momentum of the molecules by this collision.
Postulates of Kinetic Theory of Gases
To derive the kinetic equation or formula, the kinetic theory of gases consists of the following postulates or assumptions,
- Gas molecules are composed of very small discrete particles. For the same gases, the mass and size of molecules are the same but the mass and size are different for different gases.
- The molecules are moving randomly in all directions of space at a variety of speeds. Some are very fast others are slow.
- Due to random motion, the gas molecules are executing two types of collisions. When it collides with the walls of the container called a wall collision but with themselves called an intermolecular collision.
- Gas molecules are assumed to be point masses. Hence the gas sizes are very small in comparison to the distance where they travel.
- Especially at low pressure, the gas molecules have no intermolecular attraction. Therefore, one molecule can exert pressure independent of the influence of other molecules.
- The pressure exerted by a gas is due to the uniform wall collisions. Hence higher the frequency of the wall collision greater the pressure of the gas. It explains Boyle’s law. When the volume is reduced at a constant temperature, wall collision becomes more frequent and pressure is increased.
- The molecular velocity constantly changes due to the intermolecular collision but the average kinetic energy of the gas molecules remains fixed at a given temperature.
Derivation of Kinetic Gas Equation
Let us take a cubic container with edge length l containing N molecules of gas of molecular mass = m, and RMS speed = CRMS at temperature T and pressure P.
Among these molecules, N1 has velocity C1, N2 has velocity C2, N3 has velocity C3 and so on.
Let us concentrate our calculation on a single molecule among N1 that has resultant velocity C1 and the component velocities are Cx, Cy, and Cz.
∴ C12 = Cx2 + Cy2 + Cz2
If the molecule collides with walls A and B of the container with the component velocity Cx and other opposite faces by Cy and Cz. Therefore, the change of momentum along the X-direction for a single collision,
= m Cx − (− m Cx)
= 2 m Cx
A rate change of momentum along X, Y, and Z-direction is 2mCx2/l, 2mCy2/l, and 2mCz2/l.
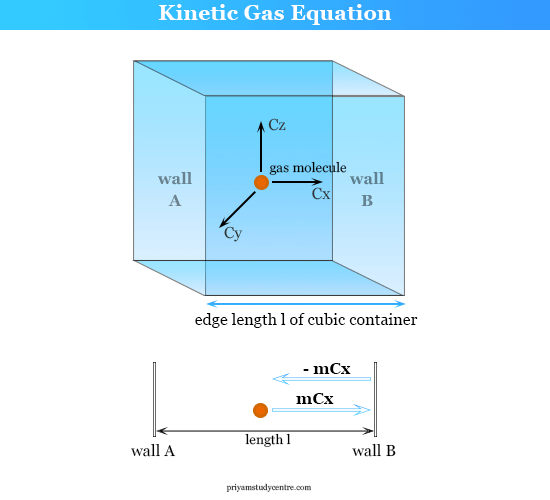
The total rate change of momentum for the molecule given above the picture,
= 2m(Cx2 + Cy2 + Cz2)/l
= 2mC12/l
For N1 molecules,
Change of momentum = 2mN1C12/l
If we consider all the molecules of the gas present in this cubic container,
A total change of momentum = 2mNCRMS2/l
Where CRMS = root means square velocity
Kinetic Gas Equation
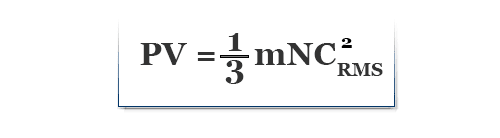
According to Newton’s second law of motion, the rate of change of momentum due to wall collision is equal to the force developed within the gases.
Therefore, P × 6l2 = (2mNCRMS2)/l
or, P × 3l3 = mNCRMS2
or, P × l3 = mNCRMS2/3
∴ PV = mNCRMS2/3
The kinetic gas equation derived from the kinetic theory of gases is used mostly to derive the root mean square velocity and density formula of the gas molecules. It is valid for any shape of the container of our environment.
Root Mean Square Speed
Root mean square speed or RMS is defined as the square root of the average of the squares of speeds of the gases. The kinetic gas equation and ideal gas law may be used to formulate the RMS velocity of the gases.
Root Mean Square Speed Formula
From the kinetic gas equation,
PV = (mN CRMS2)/3
where mN = M = molecular mass of the gases.
The ideal gas equation for 1 mole gas,
PV = RT
Therefore, 3RT = M × CRMS2
or, CRMS2 = 3RT/M
Root Mean Square Velocity of Oxygen and Hydrogen
From the above equation, root means square velocity (RMS) depends mostly on the molar mass and temperature of the gases. Therefore, at a given temperature RMS velocity decreases with the increasing molecular weight of gas molecules.
For oxygen, CRMS2 = 3RT/16
For hydrogen, CRMS2 = 3RT
∴ CRMS2 for oxygen/CRMS2 for hydrogen = 1/16
or, CRMS for oxygen/CRMS for hydrogen = 1/4
Hence the RMS velocity of the hydrogen molecule is four times greater than the oxygen molecule.
Problem: Calculate the pressure of 1023 gas molecules each of the molecules having mass = 10−22 g and a container of volume = 1 dm3. Given CRMS 105 cm s−1.
Solution: Numer of molecules (N) = 1023
mass (m) = 10−22 g = 10−25 Kg
volume (V) = 1 dm3 = 10−3 m3
CRMS = 105 cm sec−1 = 103 m sec−1
From the kinetic gas equation,
Pressure (P) = (10−25 × 1023 × 10−6)/(3 × 103)
= 0.333 × 107 Pascal (Pa)
Kinetic Energy of Gases Formula
Average Kinetic Energy Formula
The average kinetic energy is defined as,
Eaverage = mCRMS2/2
However, from the kinetic gas equation,
PV = (2 × N × Eaverage)/3
The ideal gas equation is PV = RT and N = N0.
∴ RT = (2 × N0 × Eaverage)/3
Hence average kinetic energy,
= 3RT/2N0 = 3kT/2
Where k = R/N0 = Boltzmann constant
= 1.38 × 10−23 J K−1
Therefore, the average kinetic energy is dependent on temperature only but independent of the nature of the gases.
Total Kinetic Energy Formula
The total kinetic energy for 1 mole gas = Avogadro number × average kinetic energy.
The total kinetic energy for 1 mole gases,
Ekinetic energy = N0 × (3RT/2N0)
= 3RT/2
For n-mole gases,
Ekinetic energy = 3nRT/2
Question: Calculate the average kinetic energy for hydrocarbon like methane gas at a temperature of 27 ⁰C.
Answer: From the kinetic theory of gases, the formula for average kinetic energy per molecule or kinetic energy of 1 mole of methane,
KEmethane = (3 × 2 × 300)/2
= 900 calories
Derivation of Gas Laws from Kinetic Gas Equation
From the average kinetic energy equation,
PV = 2NEaverage/3, but Eaverage = k’T
From the above two equations,
PV = 2Nk’T/3
Such energy equation calculates the necessary deductions of gas law like Boyle’s, Charles’s, and Avogadro’s law.
Charles Law from Kinetic Gas Equation
From the energy equation,
PV = 2Nk’T/3
When the pressure is kept constant, V ∝ T because N and k’ have constant values. Hence at constant pressure, the volume of the gas is proportional to its kelvin temperature. Therefore, Charles’s law can be derived from the kinetic gas equation.
Boyle’s Law from Kinetic Gas Equation
From the energy equation, when the temperature is kept constant, PV = constant. Hence the volume of the gas is inversely proportional to its pressure. Therefore, Boyles’s law can be derived from the kinetic gas equation.
The postulates or assumptions of the kinetic molecular theory of gases and the kinetic gas equation or formula are also used to calculate the kinetic energy, density, diffusion, or effusion of gas molecules.