Graham’s Law of Diffusion
Graham’s Law of diffusion and effusion in chemistry was proposed by Scottish physical chemist Thomas Graham in 1948 to study the rate of diffusion and effusion for gases and liquid molecules. According to Graham’s law, at constant temperature and pressure, the rates of diffusion or effusion of different gases are inversely proportional to the square root of their densities. It is used mainly for the partial separation of the components in a gas mixture. Let at constant temperature and pressure, the rate of diffusion or effusion of the gas molecules = r and density = d. According to Graham’s law, r = k/√d where k is a gas constant.
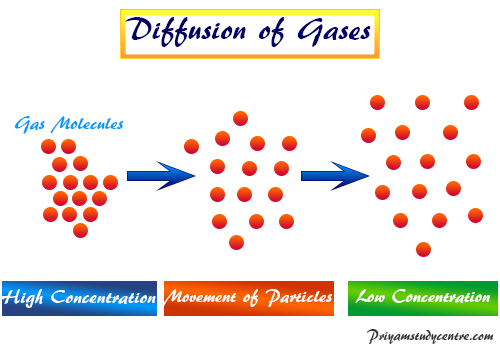
What is Diffusion?
Diffusion is the movement of gas molecules from high concentration to low concentration. It occurs due to the random movement of the gas molecules.
The phenomenon of diffusion is the tendency for any substance to spread uniformly throughout the space available to it.
What is Effusion?
Effusion is the process in which a gas passes out through a pinhole in the wall of the container with a very small diameter. The diameter of the pinhole is less than that of the mean free path of the gas molecules.
The escape of the gas is due to the pressure difference between the container and the outer environment. In learning chemistry or physics, the rate of effusion is used for the calculation of the density, pressure, and temperature of the gases.
Graham’s Law Formula
Let at constant temperature and pressure, r1 and r2 are the rates of diffusion or effusion of two gases having densities d1 and d2.
According to Graham’s law,
r1 = 1/√d1 and r2 = 1/√d2
∴ r1/r2 = √d2/√d1
How to Calculate Rate of Diffusion?
Let at constant temperature and pressure, r1 and r2 be the rates of diffusion of two gases having molar mass M1 and M2 and densities d1 and d2.
According to Graham’s law,
r1/r2 = √d2/√d1
However, the density of the gases is proportional to the vapor density. Therefore, density(d) ∝ vapour density (D)
Again we know that molecular mass = 2 × vapour density or M = 2D
Therefore, r1/r2 = √M2/√M1
This formula is used to calculate the rate of diffusion in terms of the molecular weight of gases.
Diffusion of Ammonia and Hydrogen chloride
The molar mass of ammonia = 17 g mol−1 and hydrogen chloride = 36.5 g mol−1.
From Graham’s law of diffusion, the rate of diffusion of ammonia molecules,
rNH3 = 1.46 × rHCl
Therefore, ammonia will diffuse 1.46 times faster than hydrogen chloride gas.
How to Calculate Rate of Effusion?
Let at constant temperature and pressure t1 and t2 be the time required for passing the same volume (v) of the two gases through the same pinhole.
v/t1 = r1 and v/t2 = r2
∴ r1/r2 = t2/t1 = √d2/√d1
The temperature and pressure are fixed and the molar volume vm of both the gases is the same.
Therefore, r1/r2 = t2/t1 = √M2/√M1
These two formulas are used for the calculation of the rate of effusion in terms of densities or molecular weight.
Problem: At constant temperature and pressure, 432 ml and 288 ml are the volumes of the two gases passing through the same pinhole with the time 36 min and 48 min respectively. If the molar mass of one gas is 64 g mol−1, how to find the molar mass of another gas by Graham’s law?
Solution: The rate of effusion,
r1 = 432 ml/36 min = 12 ml min−1
r2 = 288 ml/48 min = 6 ml min−1
The molar mass, M2 = 64 g mol−1
Therefore, from the Graham law,
molar mass (M1) = 64/4 = 16 g mol−1
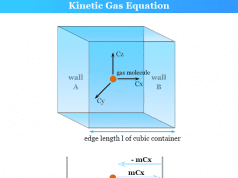
Graham’s Law of Diffusion from Kinetic Gas Equation
The rate of diffusion or effusion is assumed to be directly proportional to the root mean square speed or any other average speed.
Therefore, from the Kinetic theory of gases and the ideal gas law, we can derive the formula of Graham’s law of diffusion or effusion.

Application of Graham’s Law of Diffusion
Graham’s Law is used for the following purposes,
- The practical application of Graham’s law is mainly used for the partial separation of the components in a gas mixture.
- If the mixture leads out a tube made of porous walls, in a given time the lighter components will diffuse out more than the heavier ones.
- By repeating the process with each separate fraction from diffusion, the concentration of one component considerably increases compared to that of the other. This process is called atmolysis. Argon has been concentrated with nitrogen in this way.
- The isotopes of neon, chlorine, bromine, oxygen, etc have been partially separated by atmolysis.
- Graham’s Law is also used for detecting marsh gas or methane from coal mines.