Quantum Numbers and Atomic Orbitals
Quantum numbers such as principal, azimuthal, magnetic, and spin quantum number are the identification number of an electron present in the atomic orbitals of an atom. In physics and chemistry, these numbers describe the energy levels and fine structure of the electromagnetic spectrum of an electron particle in an atom. Three quantum numbers such as principal, azimuthal, and magnetic quantum numbers are necessary to study the size shape, size, and orientation of s, p, d, and f orbital. We have seen that the Bohr model could not explain the fine structure of the hydrogen spectrum. He indicates only one quantum number of an atom. In learning chemistry or physics, it is not sufficient to explain the absorption or emission spectrum of various atoms. Therefore, we need four quantum numbers to explain various spectral lines in an atom of periodic table elements.
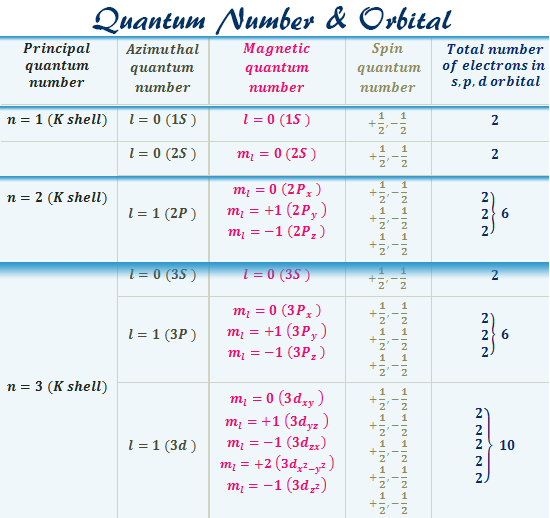
Quantum Numbers Chart
A quantum numbers chart is used to describe an electron in an atom by four different quantum numbers. The first three quantum numbers (n, l, ml) specify the particular orbital but the fourth quantum number specifies how many electrons can occupy that orbital.
Principal Quantum Number
The principal quantum number describes the set of energy levels or the principal shell to which an electron can stay. It is denoted by ‘n’. The principal quantum number is used to determine the size of an atom and the energy of an electron.
- For the hydrogen atom, the energy is fixed because it contains only one electron.
- For multielectron atoms, the energy of each electron depends mostly on the value of the principal quantum number (n).
- When the value of n increases, the radius or nucleus-electron separation increases. Therefore, the size of the orbital also increases.
How to Find Principal Quantum Number?
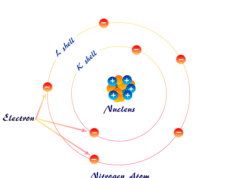
The principal quantum number (n) is always an integer having the value from 1 to ∞. The letters K, L, M, … are also used to derive the value of n.
When n = 1, 2, 3, …, the latter K, L, M, … are used to designate the value of n. Therefore, if n = 3, the electron may reside in M-shell.
Azimuthal Quantum Number
The azimuthal quantum numbers were introduced by Sommerfeld in his atomic structure to derive the angular momentum of an electron in an elliptical orbit. It describes the geometric shape of an orbital or electron wave. The azimuthal quantum number is denoted by the letter ‘l’.
How to Find Azimuthal Quantum Number?
The azimuthal quantum number (l) can have any value from o to (n−1) for a given value of n. The total number of different values of l is equal to n.
- When n = 1, l = 0 (only one value)
- When n = 2, l = 0, 1 (two values)
- If n = 3, l = 0, 1, 2 (three values)
- When n = 4, l = 0, 1, 2, 3 (four values)
Total values of l for a given value of n define the total number of subshells present in the main energy level of an atom.
- In 1s designation, the number 1 stands for the value of n and the letter s denotes l = 0.
- Similarly, in the 2p designation, the number 2 stands for the value of n and the letter p denotes l = 1.
- For 3d designation, the number 3 stands for the value of n and the letter d denotes l = 2.
- For the 4f designation, the number 4 stands for the value of n and the letter d denotes l = 3.
Various azimuthal quantum numbers and atomic orbitals designations are given below the table,
| Value of n and main shell designation | Value of l | Sub shell designation | Total number of subshells in the main shell |
| n = 1 (K-shell) | l = 0 | 1s | 1 |
| n = 2 (L-shell) | l = 0 | 2s | 2 |
| l = 1 | 2p | ||
| n = 3 (M-shell) | l = 0 | 3s | 3 |
| l = 1 | 3p | ||
| l = 2 | 3d | ||
| n = 4 (N-shell) | l = 0 | 4s | 4 |
| l = 1 | 4p | ||
| l = 2 | 4d | ||
| l = 3 | 4f |
Magnetic Quantum Number
Bohr’s one electronic model could not explain the splitting of a single spectral line into several closely spaced lines in the presence of a magnetic field or electric field.
According to Linde, the presence of more lines in the spectrum indicates that the energy levels are further subdivided. This subdivision gives an additional quantum number which is called a magnetic quantum number.
How to Find Magnetic Quantum Number?
Magnetic quantum is denoted by the symbol ‘m’ or ml. The total values of m depend on the values of l. For a given value of l, m can have any integral value between +l to −l.
| Subshell (orbital) designation and value of l | Value of m | Subshell designation | Total number of m in a given l = (2l + 1) |
| s-orbital (l = 0) | 0 | s | 1 |
| p-orbital (l = 1) | +1 | px | 3 |
| 0 | pz | ||
| −1 | py | ||
| d-orbital (l = 2) | +2 | dx2−y2 | 5 |
| +1 | dxz | ||
| 0 | dz2 | ||
| −1 | dyz | ||
| −2 | dxy | ||
| f-orbital (l = 3) | +3 | fx(x2−3y2) | 7 |
| +2 | fz(x2−y2) | ||
| +1 | fxz2 | ||
| 0 | fz3 | ||
| −1 | fxyz | ||
| −2 | fyz2 | ||
| −3 | fy(3x2−y2) |
Spin Quantum Number
When spectral lines of hydrogen, lithium, sodium, and potassium are observed by the instrument of high resolving power, each of the lines of the spectral series was found to consist of a pair of lines known as a double line structure. To identify these double-line structures, another quantum number is necessary. It is known as a spin quantum number.
- According to Uhlenbeck and Goudsmit, the electron moves around the nucleus or rotates around its axis either in a clockwise or anticlockwise direction.
- The spinning of an electron about in its axis adds to the angular momentum of the electron. Therefore, the angular momentum of an electron is not only due to the rotational motion but also due to the spinning of an electron.
Orbitals Diagram
Atomic orbitals define the basic building blocks of an atom where an electron can stay. According to the wave model, an orbital is defined as a region in space where the probability of finding an electron is maximum.
It is difficult to represent the pictorial representation of an orbital on two-dimensional paper. It is generally represented by a shaded figure. The intensity of shading is proportional to the probability of finding an electron in the shading space.
According to the wave model in quantum mechanics, the wave function of the electron in an atom is called orbital. However, the probability of finding an electron in space around the nucleus involves two orbital aspects,
- Radial probability: It is the probability of finding an electron within the spherical shell between r and (r + dr).
- Angular probability: The angular probability function describes the basic shape of an orbital or the number of lobes present in an orbital.
Shape of Orbitals
There are various shapes and sizes of s, p, d, and f orbitals. When an orbital has a small size, the chance of finding the electron near the nucleus is maximum.
Shape of s Orbital
For s-orbital, l = 0 and m = 0, it indicates that s-orbital has only one orientation. Therefore, the electron cloud distribution in s-orbitals is spherically symmetrical.
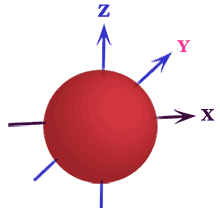
The s-electron has no angular dependence because the relevant wave function is independent of angles θ and Φ. Therefore, an equal chance of discovering the electron in any direction from the nucleus.
Shape of p Orbitals
For p-orbital, l = 1 and m = −1, 0, +1. Therefore, the p-orbitals have three orientations represented as px, py, and pz.
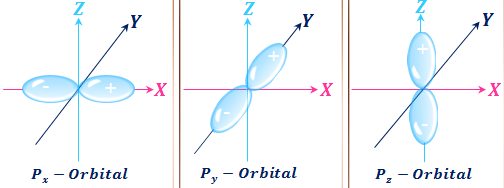
- The orbitals designation px, py, and pz are mutually perpendicular to each other. They are concentrated along their respective coordinate axes x, y, and z.
- The dumb-bell-shaped p-orbital has two lobes touching each other at the origin.
- These lobes are completely symmetrical along their respective coordinate axis. For example, the two lobes of the pz orbital are symmetrical along the x-axis.
The two lobes of a p-orbital can be separated by a plane containing the nucleus of an atom. Such a type of plane is called a nodal plane. Such a plane has zero electron density.
Shape of d Orbitals
The d-orbital of an atom is obtained when the azimuthal quantum number (l) = 2. Therefore, when l = 2, m = −2, −1, 0, +1, +2. It indicates that the d-orbital has five orientations. These five d-orbitals are named, dxy, dxz, dyz, dx2 − y2, and dz2.
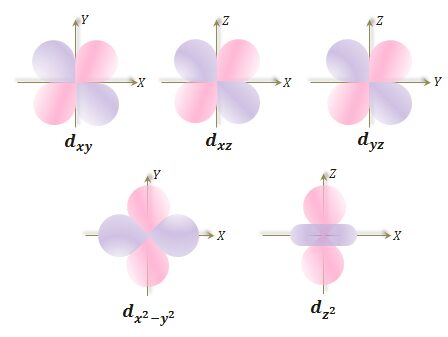
- In dxy, dxz, and dyz, the lobes are concentrated in between the appropriate coordinate axis.
- In dx2 − y2, the lobes lie along the x and y-axis.
- For dz2, there are two lobes along the z-axis and a ring in the xy plane.
Shape of f Orbitals
The pictorial representation of the f-orbital is very complicated. For f-orbital, the azimuthal quantum number (l) = 3 and magnetic quantum numbers = +3, +2, +1, 0, −1, −2, −3. Therefore, f-orbital has five orientations in space.
The quantum numbers and atomic orbital designation of f-subshell are given below in the table,
| l = 3 (f-orbital) | m = +3 | fx(x2−3y2) |
| m = +2 | fz(x2−y2) | |
| m = +1 | fxz2 | |
| m = 0 | fz3 | |
| m = −1 | fxyz | |
| m = −2 | fyz2 | |
| m = −3 | fy(3x2−y2) |
Frequently Asked Questions (FAQs)
What are the four quantum numbers of the 19th electron of chromium in the periodic table?
The atomic number of chromium is 24. Therefore, the electron configuration of chromium is 1s2 2s2 2p6 3s2 3p6 4s1 3d5.
From the above electron configuration, the 19th electron means 4s1 electron. Therefore, the calculated four quantum number for 19th electron, n = 4, l = 0, m = 0, s = +½.
Identify the correct set of quantum number for the valence electron of rubidium.
The valence electron of rubidium means 5s1 electron of rubidium atom. Therefore, the correct set of four quantum numbers for the valence electron of the rubidium atom is 5, 0, 0, +½.
How many electrons in an atom have the following quantum number n = 4 and l = 1?
4p atomic orbital has quantum numbers n = 4 and l = 1. Therefore, 6 electrons in an atom have the quantum numbers n = 4 and l = 1.
How many possible numbers of atomic orbitals when the principal quantum number is equal to four?
When the principal quantum number is 4, the azimuthal quantum numbers are equal to 0 (4s), 1 (4p), 2 (4d), and 3 (4f).
Therefore, the numbers of possible orbitals when the principal quantum number is equal to four = [1 (4s) + 3 (4p) + 5 (4d) + 7 (4f)] = 16.
How many possible orbitals are there when n = 3, l = 1, and ml = 0?
Such quantum numbers set designated 3s orbital of an atom. Therefore, with these quantum numbers set the number of possible atomic orbitals equal to one.