Thermodynamic Definition of Entropy
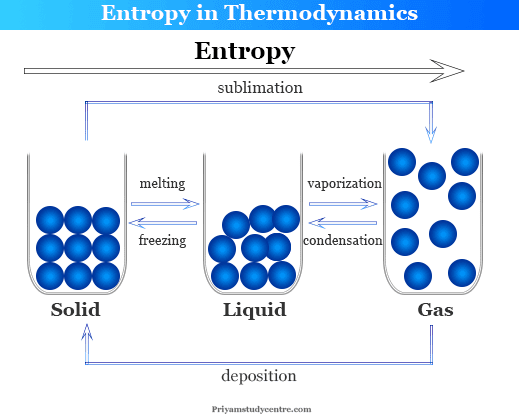
Entropy in chemistry is the thermodynamics property related to the tendency of the system towards the transformation of the states of matter. It measures the thermal energy of the system per unit temperature that is unavailable for doing useful work. In learning chemistry, entropy is the thermodynamic property that measures the randomness or chaotic condition of the system. According to the Clasusious definition, entropy (S) is a state function and entropy change can be expressed by the equation or formula, dS = dqr/T, where dqr is heat change that occurs reversibly and T is the temperature at which heat change occurs. From the molecular viewpoint, we see that the randomness of the molecules increases from solid to liquid to gases. When a substance changes its phase from solids to liquids to gases, the entropy increases from solid to liquid to gas.
Examples of Entropy
If we lose a quantity of yellowish-green chlorine gas in the corner of the room. The gas speared in all directions of the room until the equilibrium or maximum entropy was reached. A similar process happens when syrup gets diluted by adding water.
Moreover, all the natural processes in our environment have a tendency to attain equilibrium by increasing the entropy of the system.
Significance of Entropy
The concept of this thermodynamics property is obtained from the unavailable energy in thermodynamics. The higher the randomness greater the entropy for molecules.
A system passes spontaneously from more orderliness to less orderliness. If the system is left to change its state spontaneously, it attains a maximum chaotic state.
Therefore, for a spontaneous process, ΔSnet of the universe (system + surroundings) increases. The system attains equilibrium when the ΔSnet is maximum.
Entropy Change Formula
According to the Clasusious definition, entropy (S) is a state function and its change can be expressed by the formula,
dS = dqr/T
where dqr = heat change that occurs reversibly
T = temperature at which heat change occurs
When heat change occurs in different temperatures,
ds = dq1/T1 + dq2/T2 + dq3/T3 + … = ∫ dqr/T
- Absorption of heat increases the entropy of the system while evaluation of heat decreases the value of S.
- For reversible adiabatic process, dq = 0. Therefore, dS = 0. It means entropy remains constant for isolated systems or adiabatic processes.
How to calculate entropy when one mole of water is heated reversibly from 27 °C to 37 °C?
When one mole of water is heated reversibly from 27 °C to 37 °C, the entropy change,
ΔS = nCpln(T2/T1)
= 1 × 18 × ln(310/300)
= 1.18 cal/deg
Change in Entropy for Isothermal Process
When heat change occurs at a constant temperature. For example, one mole of ice changes into liquid water at 0 °C and 1 atmosphere pressure.
Therefore, entropy change,
(ΔS) = S2 − S1
= (18 × 80)/273 cal/deg
= 5.27 cal/deg
Entropy Change in Universe
In a reversible process, heat absorbed by the system is equal to that lost from the surroundings. Let dqr amount of heat be absorbed by the system and − dqr heat lost from the surroundings at temperature T.
Therefore, ΔSsystem = dqr/T
Similarly, ΔSsurrounding = − dqr/T
From these two equations, the ΔS of the universe,
ΔSunivese = ΔSsystem + ΔSsurrounding = 0
Basic Thermodynamic Equations
The 1st law of thermodynamics for a reversible process,
dqr = dU + PdV
From the 2nd law of thermodynamics,
dS = dqr/T
or, TdS = PdV
Combining both the forms, we have the relation,
TdS = dU + PdV
Again dH = U + PV
or, dH = dU + PdV + VdP
∴ dH = TdS + VdP
These two equations are called basic thermodynamic equations for states.
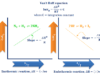
Carnot Cycle Efficiency

French engineer Sadi Carnot (1824) studied what quantity of work is obtainable from the heat in the Carnot engine. He takes the ideal gas in a cylinder fitted with a frictionless movable piston. The Carnot cycle operates in reversible paths given above the picture.
From Carnot cycles, we can conclude that heat change/temperature = constant for the change of two definite states and independent of path change. For the whole cycle of operation, heat change/temperature is equal to zero.
Entropy and Carnot Cycle
From the Carnot cycles,
dq1/T1 = dq2/T2
where dq1 = energy supplied to the Carnot cycle at temperature T1
However, the Carnot cycle fails to convert dq2 heat into useful work. It is rejected from the sink at T2. The unavailable energy for the cycle = dq2. Therefore, the unavailable energy for the Carnot cycle = T2dS.
When a system absorbs a certain amount of heat in the reversible process, a part of the absorbed energy can be utilized for producing work. The remaining part goes to increase the randomness or entropy of the system.