Law Mass Action

What is Law of Mass Action?

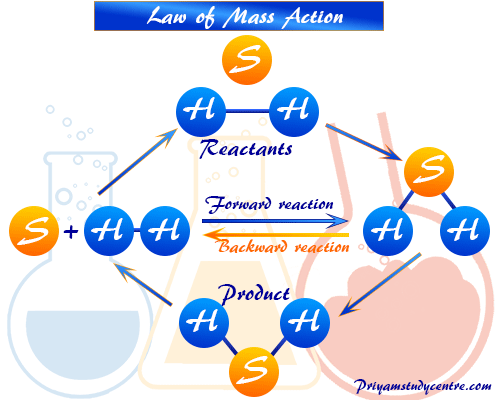
Law of Mass Action or Mass Action Law formula in chemical equilibrium was first developed by two Norwegian chemists, Guldberg and Waage in 1867. They derive a quantitative equation to calculate the equilibrium constant of a reaction in terms of molar concentration or active masses of reactants and products in chemistry. The Law of Mass Action states that at a constant temperature, the rate of a chemical reaction is proportional to the active masses of reacting molecules.

The definition and expression of active masses in Mass Action Law is an important consideration to help equilibrium chemistry.

Dynamic Equilibrium in Chemistry

The mass of action law in equilibrium chemistry was defined before the thermodynamics approach developed. The Law of Mass Action recognized that the chemical equilibrium is a dynamic, not static equilibrium because the reaction rate of the forward reaction is equal to the reaction rate of the backward reaction.

How the system behaves if any parameter like temperature, pressure, or chemical catalyst of the system at equilibrium changes can be described by different formulas like Le Chatelier Principle and Van’t Hoff equation.

Active Mass in Chemistry

For ordinary systems of dilute solution and gases, the active mass may be molar concentration and partial pressure but for pure crystalline solid or liquid, the active mass is taken as unity according to the Law of Mass Action.

Molar Concentration

Concentration or active masses formula effect by thermodynamics Mass Action Law. When the solution is dilute and the system behaves ideally the concentration is represented as the molar concentration.

The unit of molar concentration is moles/lit. For example, the esterification of acetic acid in the alcohol solution is derived from the molar concentration unit.

Partial Pressure

Partial gas pressure is expressed in the atmosphere for the gas molecule concentration when the pressure of the system is very low.

For example, the formation of water or the formation of carbon dioxide gas, active mass expressed in molar concentration, and partial pressure by the law of mass action.

For pure solid and pure liquid, active mass or concentration is assumed to be unity since their mass does not affect the rate of reaction.

Rate Constant Formula

Let us state the equilibrium formula and mass of action law to a general chemical reaction,
A + B ⇆ C + D

As the reaction proceeds in the forward direction, the concentration of reactants decreases, and the forward reaction rate also decreases. But when the products are getting accumulated in the system, the reverse reaction also starts.

Rate of forward reaction,
R_f ∝ C_A × C_B
∴ R_f = k_f × C_A × C_B

Rate of backward reaction,
R_b ∝ C_C × C_D
∴ R_b = k_b × C_C × C_D

Where C_A, C_B, and C_C, C_D are the concentration of forwarding and reverse reactions respectively in molar units. K_f and K_b are the rate constants at a given temperature.

Concentration Equilibrium Constant Expression

As the reactions proceed, the forward reaction rate decreases but the reverse reaction rate increases and attains a state when they are equal concentration.

The point where forward and reverse reaction rates are equal is called the equilibrium point of the chemical reaction. There will be no further change in the concentration of the system.

At equilibrium,
R_f = R_b
or, k_f × C_A × C_B = k_b × C_C × C_D

Where C_A, C_B, C_C, and C_D are the equilibrium point concentrations of reactants and products. The term, k_f/k_b = k_c = concentration equilibrium constant.

How to Calculate Equilibrium Constant?

Let us consider a general balanced chemical reaction to define Mass Action Law in terms of concentration for learning chemistry,
Ɣ₁A₁ + Ɣ₂A₂ ⇆ Ɣ₃A₃ + Ɣ₄A₄
where Ɣ₁, Ɣ₂, Ɣ₃, and Ɣ₄ are stoichiometric coefficients
∴ k_c = (C₃^γ3 × C₄^γ4)/(C₁^γ1 × C₂^γ2)

where k_C = concentration equilibrium constant of the reaction and C₁, C₂, C₃, and C₄ are the equilibrium concentration of the reactants and product.

The values of the k_C of a chemical reaction from the Mass Action Law affect the mode of writing or balance of the stoichiometric chemical equation.

If a chemical equation is multiplied by n then the general rule for writing equilibrium concentration n will be raised to the power,
k_C = (k′_C)ⁿ
where k_C, and k′_c are not equal in magnitude

Therefore, the calculation of the concentration equilibrium constant depends on the modes of balancing chemical equations.

Pressure Equilibrium Constant Expression

When all the reactants and products are the gas phase obey the ideal gas law, the concentration formula is expressed in partial pressure by the Mass Action Law.

Let the chemical equation for the above expression,
Ɣ₁A₁ + Ɣ₂A₂ ⇆ Ɣ₃A₃ + Ɣ₄A₄
where Ɣ₁, Ɣ₂, Ɣ₃, and Ɣ₄ are stoichiometric coefficients.
∴ k_P = (P₃^γ3 × P₄^γ4)/(P₁^γ1 × P₂^γ2)

Where k_P = pressure equilibrium constant of the reaction. P₁, P₂, P₃, and P₄ are the equilibrium concentrations in terms of the partial pressure of reacting components.

Equilibrium Constant in Terms of Mole Fraction

Let us consider a general balance chemical reaction to define Mass Action Law in terms of mole fraction,
Ɣ₁A₁ + Ɣ₂A₂ ⇆ Ɣ₃A₃ + Ɣ₄A₄
where Ɣ₁, Ɣ₂, Ɣ₃, and Ɣ₄ are stoichiometric coefficients
∴ k_x = (x₃^γ3 × x₄^γ4)/(x₁^γ1 × x₂^γ2)

Where k_x = equilibrium constant in terms of mole fraction and x₁, x₂, x₃, and x₄ is the concentration in terms of mole fraction of reacting components derived from the Mass Action formula.

Relation Between k_p and k_c

Let us consider the general equilibrium concentration reaction which expresses the relation between k_P and k_C gas and liquid phase by Mass Action Law.

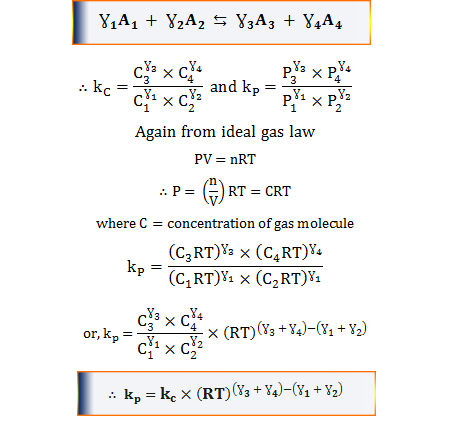
Formation of Hydrochloric Acid

Formation of hydrochloric acid solution from hydrogen and chlorine molecules. In this reaction, the total number of reactant molecules, and of resultant molecules are the same.

H₂ + Cl₂ ⇆ 2 HCl
k_P = k_C (RT)^2-(1+1) = K_C

Dissociation of Phosphorus Pentachloride

For the reactions in which the number of molecules of reactants differs from the resultant molecules of the chemical reaction.

PCl₅ ⇆ PCl₃ + Cl₂
k_P = k_C (RT)^{(1+1) -1} = K_C RT

The expression of k_P and k_C of the above chemical reaction in terms of concentration derives from the mass of action law formula.

Relation Between k_p and k_x

k_P = k_x (P)^Δγ

k_p = concentration equilibrium constant and k_x = equilibrium constant in terms of mole fraction given from the Law of Mass Action.