What is Chemical Kinetics?
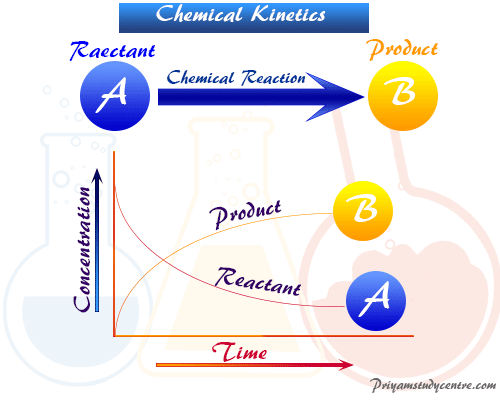
Chemical kinetics is the branch of physical science concerned with the rate change of concentration of reactants and products of chemical reactions per unit time. Such studies of kineties enable us to understand the mechanism by which the reactions occur. In chemical kinetics, time variables are introduced. Therefore, the rates law in chemical kinetics defines the equation, formula, reaction mechanism, and molecular pathways in chemistry, biology, cosmology, or engineering.
In chemical equilibrium, only the initial and final states were considered. The energy relationship between the reactants and products is governed by thermodynamics law.
Types of Chemical Reactions
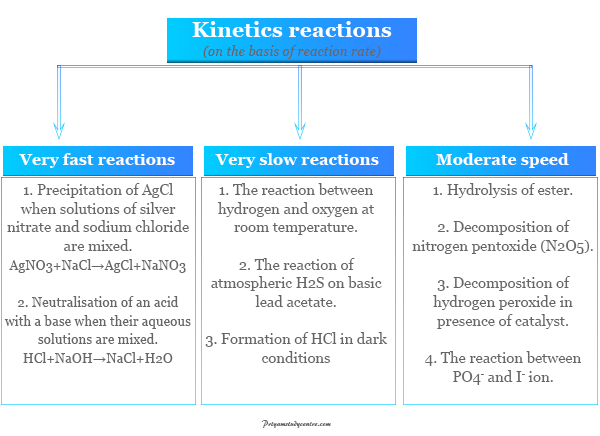
On the basis of the speed of chemical kinetics reaction, there are three types,
- Very fast reactions
- Very slow reactions
- Moderate speed reactions
Fast and Slow Chemical Reactions
- Very fast reactions: Oxidation reduction or redox reaction are examples of very fast reactions.
- Very slow reactions: The formation of hydrochloric acid in dark conditions is an example of a very slow reaction. It can not be studied under chemical kinetics.
- Moderate speed reactions: Only a moderate rate of reaction is discussed under kinetic study. Hydrolysis of ester, decomposition of nitrogen pentoxide (N2O5), and the reaction between PO4− and I− are examples of moderate rate reactions that are studied under chemical kinetics.
From a kinetic standpoint, the chemical reactions are classified into two groups,
- Homogeneous: It occurs entirely in one phase.
- Heterogeneous: The chemical transformation takes place on the surface of the chemical catalyst.
Importance of Chemical Kinetics
There are two main importance for studying the rate equations in chemical kinetics.
- The first is the practical importance that able to predict how quickly a reaction mixture moves to equilibrium in chemistry. Therefore, it depends only on the external factor used to precede the reaction.
- The second is the theoretical importance of kinetic reactions that define the chemical formulas and mechanisms in physical chemistry. It can analyze the chemical reaction in many elementary steps.
Rate of reaction formula
The differential rate equations of chemical reaction in kinetics depend on the change of concentration of reactants and products at any instant in time.
Let a simple kinetic reaction,
A → B
The rate in terms of reactant = − d[A]/dt
The rate in terms of product = d[B]/dt
Negative signs are used to show the decrease in the concentration of reactants with time. But the rate is always a positive quantity and it decreases with time.
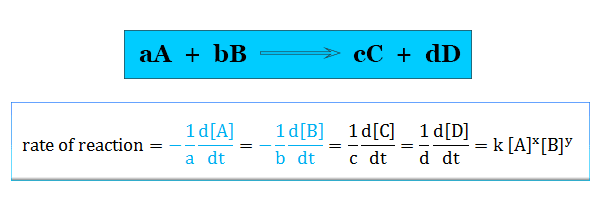
A complication arises if we consider the reaction,
A + 2B → 3C + D
In this chemical reaction rate of decrease of B is twice the rate of decrease of A. To resolve this complication we mention the rate of reaction in terms of a particular component given in the picture,
Question: In a chemical reaction, N2 + 3H2 → 2 NH3 the rate of (d[NH3]/dt) = 2 × 10−4. How to calculate the value of (−d[H2]/dt) by kinetics equation?
Answer: From the rate equation for the formation of ammonia from nitrogen and hydrogen,
d[H2]/dt = (3/2) × 2 × 10−4 mol lit−1 sec−1
= 3 × 10−4 mol lit−1 sec−1
Unit of rate of reaction
In physical chemistry, the rate of reactions in chemical kinetics is defined as the rate of change of concentration of reactants and products at any instant in time.
The unit of rate = unit of concentration/unit of time. Therefore, the unit of the rate of the reaction is mol lit−1 s−1 or mol m−3 s−1.
Factors Affecting Rate of Reaction
Several types of physical and chemical factors affect the rate of a kinetics reaction,
- The rate of reactions also depends on the active mass, or concentration of the reactants and products derived by mass of action law chemistry.
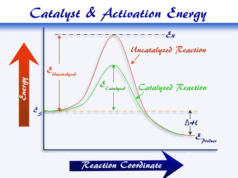
- The temperature dependence is derived from the Arrhenius equation of activation energy.
- The rate of reactions also depends on, the presence of a chemical catalyst in a chemical reaction.
- Degree of fineness of reactants.
- Absorption of radiation of suitable frequency derived in the photochemical reaction.
Kinetics Rate Equations
In Chemistry, the mass of action law guides the basis of the formulation of kinetic rate equations. But the rate equation can only be formulated on the basis of the experimental chemical kinetics data report.
The decomposition of hydrogen peroxide into hydrogen and oxygen is represented as,
2H2O2 → 2H2O + O2
From the mass action law and kinetic rate equation,
− d[H2O2]/dt = k [H2O2]2
But the experiment shows the rate equation,
− d[H2O2]/dt = k [H2O2]
where k = constant, called the rate constant for a specific reaction.
The single power of concentration controlled the decomposition of hydrogen peroxide. Therefore, the decomposition of hydrogen peroxide is first-order chemical kinetics because only one concentration term is used to express the rate equation.
For a general reaction,
aA + bB → cC + dD
Rate of chemical reaction = k × CAm × CBn
Where values of m and n depend on the experimental report of kinetics data. It does not depend on the theoretical values of a and b.
How to Calculate the Rate Constant?
If a kinetic reaction is expressed as,
A → Product
The rate equation for this reaction,
− d[A]/dt = k [A]n
where n = order of the reaction
Unit of Rate Constant
The unit of rate constant in kinetics,
unit of k = (unit of concentration)1-n/unit of time
| Order of kinetics reaction | Unit of rate constant |
| nth order kinetics | (mol L−1)1−n s−1 |
| zero order kinetics | mol L−1 s−1 |
| first order kinetics | s−1 |
| second order kinetics | L mol−1 s−1 |
Half-life in Chemical Kinetics
When the chemical reaction precedes, the concentration of reactant decreases, and productivity increases. But after a certain period of time the value of the reactant one haft of the initial concentration. It is called half-life.
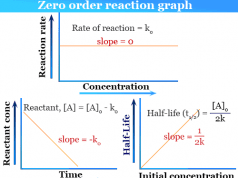
The integrated rate law of the zero-order kinetics which is used to derive half-life equations in chemistry,
x = k0 × t
When, t = t½ , x = x/2
∴ t½ = x/2k0
where x = initial concentration of reactant
Application of Chemical Kinetics
In learning chemistry, the application of rate law in chemical kinetics serves mainly three purposes.
- It predicts the rates of reactions at a given concentration from the knowledge of the rate constant.
- Rate law helps to build up the possible mechanism of a chemical reaction.
- From the rate laws studies, we can clarify the kinetics of the chemical reaction as first, second, or third-order.
