What is Planck’s Quantum Theory?
Planck’s quantum theory was presented by Max Planck on December 14, 1900. According to Planck’s quantum theory, an atom or molecule absorbs or emits radiation discontinuously in the form of energy packets called bundles or quanta. Planck quantum theory successfully explained the electromagnetic spectrum distribution of black body radiation.
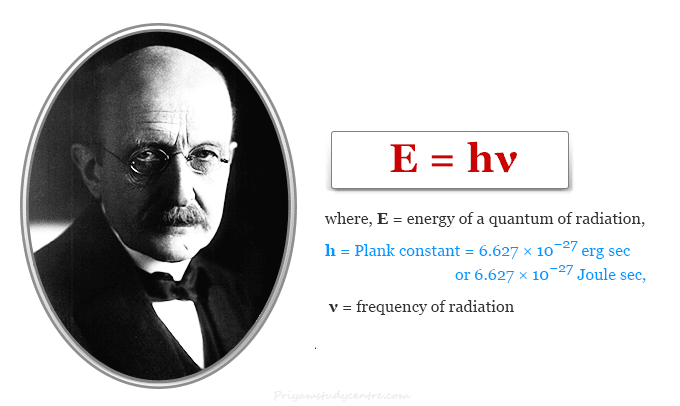
A quantum of energy emitted by light is called a photon. A black body absorbs completely all electromagnetic radiation falling on it and conversely, it emits radiations of all wavelengths. Planck quantum theory consists of the following postulates,
- According to Max Planck quantum theory, an oscillator absorbs or emits radiation discontinuously in the form of energy packets called quanta. Quanta may be behaving like a stream of particles possessing mass, energy, and momentum. The energy of a quantum of radiation,
E = hν
where h = 6.627 × 10−27 erg sec or 6.627 × 10−27 Joule sec and ν = frequency of radiation.
Therefore, the magnitude of a quantum is not fixed and it depends on the frequency of the oscillator. - An oscillator has a definite amount of energy in discrete levels, called energy levels.
- The energy (En) of the nth energy level is an integral multiple of a quantum (hν).
Therefore, En = nhν
where n = integers having the values 1, 2, 3, 4, 5, etc.
Energy of Photon
The amount of energy carried by a single photon is called photon energy. From Planck’s quantum theory, the amount of energy of a photon is directly proportional to its frequency or inversely proportional to its wavelength.
∴ E ∝ ν
or, E = hν
where ν = frequency of radiation
h = Planck constant.
Therefore, the energy of photons is only multiples of hν. If the frequency of photons increases, its energy also increases.
Again ν = c/λ
Therefore, E = hc/λ
where, c = velocity of light = 3 × 108 m s−1
λ = wavelength of photons
Hence higher energy photons show lower wavelengths. Photon energy can be derived from any unit of energy.
Problem: A 100 watt sodium vapour lamp emits yellow light with wavelength (λ) = 590 nm. Calculate the number of photons emitted per second by using the Planck quantum equation.
Solution: The energy of the yellow photon,
E = hc/λ = 3.37 × 10−19 J
Therefore, the number of photons emitted from 100 watt sodium vapour lamp = 100/3.37 × 10−19
= 2.967 × 1020
Black Body Radiation and Planck’s Quantum Theory
A black body or blackbody in physics is an idealized surface that absorbs all radiant energy falling on it. The name “black body” is given because it absorbs radiations of all wavelengths.

Blackbody radiation defines the spectrum of light emitted by any heated object. Tungsten filament lights provide a continuous black body spectrum.
When a solid is heated, it emits radiation with a wide range of wavelengths. Therefore, a solid may change its colour with the increase in temperature. The colour changes happen due to changes in the frequency region. It changes from a lower frequency region (red) to a higher frequency region (blue).
Hence, we can say radiation density for the black body is a function of temperature. At a given temperature, the intensity of radiation increases with an increase in wavelength. It goes to a maximum value and then decreases with an increase in the wavelength.
This phenomenon may not be explained by Maxwell’s theoretical consideration. Therefore, in 1900 the German physicist Max Planck proposed Planck’s quantum theory for the calculation of the blackbody radiation.
Planck Equation
The energy of a photon can be calculated from Planck’s equation, E = hν, where, ν = frequency of the radiation and h = 6.625 × 10−34 J s.
Planck’s equation helps to calculate the energy of photons when their frequency is known. But if the wavelength (λ) is known, we can use the equation,
E = hc/λ
where c = velocity of light
In 1924, de-Broglie combined Planck’s quantum theory and Einstein’s theory of relativity to formulate a relation known as the de-Broglie relation,
λ = h/mc = h/p
where mc = p = momentum of the photon
The de-Broglie relation connects the wave nature (λ) and particle nature (p) of light.
Einstein Photoelectric Equation
In 1905, Albert Einstein explained the photoelectric effect on the basis of Planck’s quantum theory. According to this theory, light is composed of discrete particles or photos having energy hν. When a photon hits the metal surface (sodium, potassium, zinc, etc), it gives up its entire energy to the electron on the surface.
The entire energy of the photon present in radiant light must be accepted by a single electron. It cannot be divided among all the electrons present on the metal surface as supposed by classical theory.
Einstein suggested that a certain quantity of energy, called work function (w) is utilized to overcome the attractive forces between the electron and the positive nuclei of the metal. The rest part of the energy goes along with the ejected electron in the form of kinetic energy.
Therefore, we can write,
hν = w + ½ mv2
It is shows that when ν = ν0, ½ mv2 = 0
Hence hν0 = w
Therefore, the Einstein photoelectric formula based on Planck’s quantum theory,
ν = hν0 + ½ mv2
The Einstein photoelectric equation explains all the observations found in the photoelectric experiment.
- It explains that irradiation or ejection of an electron is instantaneous. The electrons eject immediately when light falls on the metal surface.
- As the intensity of the radiation increases, the number of photons falling per unit time on a metal surface is increasing. Therefore, the number of electrons ejecting per unit of time also increases.
Planck’s quantum theory presented by Max Planck successfully explains the phenomena such as black body radiation, photoelectric effect, wave-particle duality, the specific heat of solids, atomic spectra, etc.