Ionic mobility in electrochemistry
Ionic mobility in chemistry is the velocity of an ion under a unit potential gradient or field strength. Therefore, ionic mobility = velocity of the ion/potential gradient or field strength. The velocity of an ion in a solution depends on the nature of the ion, the concentration of the solution, the temperature, and the applied potential gradient. It is related to the ionic conductance of the solution. The moving boundary method is used to measure the mobility of an ion directly. It contains a tube of a uniform cross-section filled with an electrolyte solution (KCl) over another solution (CdCl2).
Ionic mobilities of some common cations and anions are given below the table,
| Cation | u × 104 | Anion | v × 104 |
| Hydrogen ion (H+) | 36.2 | Hydroxide ion (OH−) | 20.5 |
| Potassium ion (K+) | 7.61 | Sulfate ion (SO4−2) | 8.27 |
| Sodium ion (Na+) | 5.20 | Chloride ion (Cl−) | 7.90 |
| Ammonium ion (NH4+) | 7.60 | Bromide ion (Br−) | 8.12 |
| Silver ion (Ag+) | 6.40 | Iodide ion (I−) | 7.96 |
| Calcium ion (Ca+2) | 6.16 | Nitrate ion (NO3−) | 7.40 |
| Magnesium ion (Mg+2) | 5.50 | Acetate ion (CH3COO−) | 4.25 |
Unit of ionic mobility
From the above formula, the unit of ionic mobility in the CGS system = cm s−1/volt cm−1
= cm2 s−1 volt−1
In the SI system, the unit of ionic mobility,
= metre2 s−1 volt−1
The limiting value of ionic mobility is obtained at infinite dilution when the interionic attraction is totally absent.
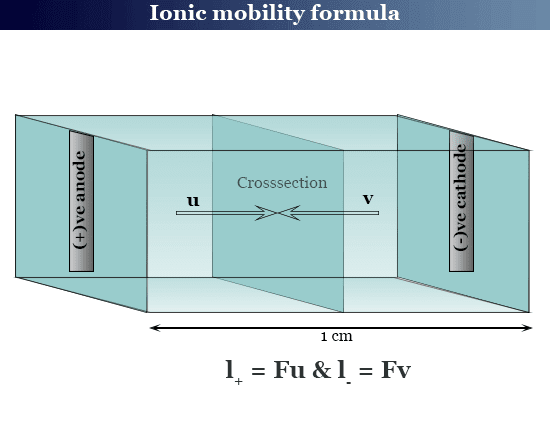
Ionic mobility formula
Let us consider a cell that contains two electrodes 1 cm apart introducing a solution containing 1g equivalent electrolyte. For an applied potential (V), let the current I flow through the cell. Since the solution obeys Ohm law.
I = V/R = λV
The solution contains one g equivalent electrolyte and the conductance (1/R) = λ.
From Kohlrausch’s law of infinite dilution,
λ = (l+ + l–)
∴ I = λV = (l+ + l−)V
= l+V + l−V
= I+ + I−
The flow of current through the cell can be analyzed from the movement of ions in the cell. Since the cell contains N/Z+ positive ions and N/Z− negative ions, N = Avogadro number, and Z+ and Z− are the valency of cation and anion respectively.
Let u and v be the velocity of cation and anion. Therefore, the current carried by the cation,
I+ = (N/Z+) × u × Z+e
= Neu
= Fu
Where Ne = F = Faraday
Similarly, the current carried by anion
I− = Fv
Equating these equations with Kohlrausch equation
I+ = l+V = Fu
I− = l−v = Fv
When V = 1 volt, velocity becomes mobility.
Therefore, we have the formula
l+ = Fu
l− = Fv
Where u and v are the ionic mobility of cation and anion respectively.
Problem: A potential of 2 volts is applied to two electrodes placed 4 cm apart. How far would a K+ ion move in one hour in a very dilute water solution of KCl at 25 °C? Given λKCl = 150 ohm−1 cm2.
Solution: Potential gradient = 2/4 = 0.5 volt cm−1.
∴ λKCl = lK+ + lCl−
= 150 ohm−1 cm2
Ionic mobility and transport number
The limiting mobility
u = l+/F but l+ = t+λ
Hence, u = t+λ/F and v = t−λ/F
At an appreciable concentration solution, u and V will be slightly less.
Experimental Measurement
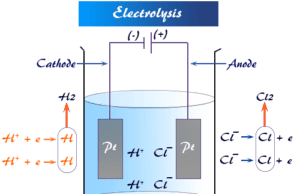
The moving boundary method is used to measure the mobility of an ion directly. A tube of the uniform cross-section is filled with an electrolyte solution (KCl) over another solution (CdCl2). The velocity of K+ > Cd+2.
A current is passed through the solution and K+ moves toward the cathode. This ion is followed by the slow-moving cadmium ion (Cd+2). Let dx be the distance up to which the boundary moves in time dt under potential gradient E. Therefore, the mobility of potassium ion (K+) = (dx/dt)/E.
Problems Solutions
Problem: The ionic conductance of lithium and potassium ions is 38.7 mho cm2/g ion and 73.5 mho cm2/g ion respectively. How long would it take for an ion of each type to move from one electrode to another (2 cm apart) of a conductivity cell? The potential difference between the two electrodes is 10 volts.
Solution:
Potential gradient = 10/2
= 5 volt cm−1
Therefore, ionic mobility of K+ = 73.5/96500 cm2 s−1 volt−1
Velocity of K+ = (73.5 × 5)/96500 cm/s
=
Similarly velocity of Li+ = (38.5 × 5)/96500 cm/s
=
Therefore, the time required for K+ to move from one electrode to another,
tK+ = 2/velocityK+
= (2 × 96500)/(73.5 × 5)
= 525 s
Similarly, tLi+ = 997 s
Problem: Conductance of KCl is 120 ohm−1 cm2 mol−1. Calculate the sum of mobilities of cation and anion. If t+ = 0.55, calculate the velocity of the cation when a potential difference of 2 volts is applied between two electrodes placed 4 cm apart.
Solution:
The sum of mobilities of cation and anion
= 120/96500
= 1.24 × 10-3 cm2 s−1 volt−1
∴ Mobility of K+ = 0.55 × 1.24 × 10−3 cm2 sec−1 volt−1
Hence the velocity of K+ = 0.55 × 1.24 × 10−3 × (2/4)
= 3.42 10−4 cm/s
Problem: Conductance of AgNO3 is 120 ohm−1 cm2 mol−1 and tNO3− = 0.55 at 25 °C. Find the velocity of Ag+ ions for an applied potential of 104 volt/cm.
Solution:
Transport number of Ag+ = 1 − 0.55
= 0.45
Therefore, the velocity of Ag+
= (0.45 × 120 × 104)/96500
= 5.59 cm/s