Ionization Energy

Ionization Energy in Periodic Table

Ionization energy or ionization potential in chemistry is the minimum amount of energy required to remove the outer electron of an isolated gaseous atom present in the periodic table of chemical elements. It is generally represented by IE or IP and measured by unit electron volt (eV) and kilojoules per mole (kJ/mol). Generally, the value of ionization energy of periodic table elements increses from left to right in a period because the nuclear charge (atomic number) of elements increses in the same direction.

The process by which an element loses an electron to convert a cation is called ionization. It can be calculated from the required energy to complete this process. Ionization is an endothermic process because energy is supplied to affect it.

For learning chemistry, the periodic table trend of ionization energy or potential is affected mainly by the following factors,

1. Atomic radius
2. atomic number
3. Charge on the nucleus
4. Filled or half-filled orbitals
5. Shielding electron
6. Oxidation number of elements

What is Ionization Energy?

The electron is raised to a higher energy level by absorption of energy from external sources. If the ionization process continues, a stage comes where the electron goes fully out of the influence of the atomic nucleus.

In simple words, ionization energy (IE) or ionization potential (IP) is the minimum amount of energy required to remove the most loosely bound electron of an isolated gaseous atom or ion of an element.

In physics, ionization energy is generally expressed by unit electron volt (eV) but in chemistry, it can be expressed by unit kilojoules per mole (kJ/mol) or kilocalories per mole (kcal/mol).

Ionization Energy Equation

Electrons are raised to higher energy levels by the transfer of energy from external sources. But if energy transfers to electrons sufficiently, electrons go fully out of the influence of the nucleus of atoms. Ionization energy can be represented by the following equation,

M (g) + IE → M⁺ (g) + e⁻

From the above equation, M = an atom of the periodic table of elements, M⁺ = cation form due to ionization, and e⁻ = electron removed from M atom.

IE is positive for neutral atoms and ionization is an endothermic process. Therefore, the ionization energy or enthalpy of the periodic table element is an endothermic reaction in thermodynamics. During the ionization process, energy is consumed by atoms.

Electron Volt to Joule

For the conversion of electron volt to joule, first, we define electron volt. The energy required by an electron falling through a chemical potential difference of one volt is called an electron volt (eV).

From the definition,
1 eV = charge of an electron × 1 volt
= (1.6 × 10⁻¹⁹ coulomb) × (1 volt)
= 1.6 × 10⁻¹⁹ Joule
1 eV = 1.6 × 10⁻¹² erg

First, Second, and Third Ionization Energies

The electrons are removed in stages one after the other from an atom or ions. Therefore, the values of successive ionization energies of an element differ one from another. The successive ionization energies can be represented as first, second, third, fourth, etc.

• First ionization energy: The amount of energy required for the removal of the first electron from a gaseous atom is called its first ionization energy (IE₁).
  M (g) + IE₁ → M⁺ (g) + e⁻
• Second ionization energy: The energy required for the removal of the second electron from a unipositive cation is called second ionization energy (IE₂).
  M⁺ (g) + IE₂ → M⁺² (g) + e⁻
• Third and fourth ionization energies: Similarly, we have to define the term third, the fourth ionization energies of periodic table elements.
  M⁺² (g) + IE₂ → M⁺³ (g) + e⁻
  M⁺³ (g) + IE₂ → M⁺⁴ (g) + e⁻

Successive Ionization Energies Values

The values of successive ionization energies increses in the following order:

IE₁ < IE₂ < IE₃ < IE₄ …

The ionization energy values increses successively because the removal of an electron from a cation having a higher positive charge is relatively more difficult.

Element	Atomic number	Electronic configuration	Successive ionization energies (kJ/mol)
			IE1	IE2	IE3	IE4	IE5	IE6	IE7	IE8
H	1	1s2	1312.0
He	2	1s2	2372.3	5250.5
Li	3	1s22s1	520.2	7298.1	11815.0
Be	4	1s22s2	899.5	1757.1	14848.7	21006.6
B	5	1s22s22p1	800.6	2427.1	3659.7	25025.8	32826.7
C	6	1s22s22p2	1086.5	2352.6	4620.5	6222.7	37831.0	47277.0
N	7	1s22s22p3	1402.3	2856.0	4578.1	7475.0	9444.9	53266.6	64360.0
O	8	1s22s22p4	1313.9	3388.3	5300.5	7469.2	10989.5	13326.5	71330.0	84078.0
F	9	1s22s22p5	1681.0	3374.2	6050.4	8407.7	11022.7	15164.1	17868.0	92038.1

Ionization Energy of Hydrogen

The energy required for completely removing an electron from hydrogen energy levels is called the ionizing energy of a hydrogen atom. Therefore, the ionized energy of hydrogen can be measured by calculating the energy difference for the transition of an electron from n = ∞ to n = 1.

From the Bohr model of hydrogen, the ionization potential of hydrogen,
IE_H = 2.179 × 10⁻¹¹ erg
= 2.179 × 10⁻¹⁸ Joule
= 13.6 eV

Ionization Energy of Helium

The electron configuration of helium 1s². The second ionization potential is found by the removal of the second electron from the 1s orbital against the nuclear charge of +2.

Hence the calculated IE of He from the Bohr energy equation,
IE_He = Z² × IE_H
= 2² × 13.6 eV
= 54.4 eV

Factors Affecting Ionization Energy

The magnitude of the ionization energy of the periodic table elements depends on the following factors,

• Charge of the nucleus
• Atomic radius
• Half-filled and filled orbitals
• Shielding effect of electrons

Atomic Radius Trend

The atomic radius decreases from left to right along a period in the periodic table. Therefore, when we move left to right along a period in the periodic table, ionization potential trends normally increase because the atomic radius decreases

When we move from top to bottom in a group the value of the potentials of chemical elements decreases with the increasing size of the atom.

Charge of the Nucleus

With the increasing atomic number, the charge on the nucleus increases. Hence the electrostatic attraction between the outermost electrons and the nucleus of an atom increases and it is comparatively more difficult to remove an electron. Therefore, ionization energy value increses with the increasing charge of an atom.

Generally, the value of ionization energy increases when moving from left to right in a period because the nuclear charge of the elements also increses in the same direction.

Element of 2nd Period	Li	Be	B	C	N	O	F	Ne
Nuclear charge	+3	+4	+5	+6	+7	+8	+9	+10
Ionization energy (kJ/mol)	520.2	899.5	800.6	1086.5	1402.3	1313.9	1681.0	2080.7

Atomic Radius and Ionization Energy

The greater the atomic radius of elements in the periodic table, the weaker will be the attraction. Hence the required energy for the removal of the electron is lower.

In the case of larger atoms, the attraction between the nucleus and the outermost electron is less. Hence it is easier to remove an electron from a larger atom than from a smaller atom.

Generally, when we move from top to bottom in a group, the ionization energy of an atom decreases with increasing atomic radii. When we move from top to bottom in a group, the number of inner shells increses, and the ionization potential tends to decrease.

Half-Filled and Filled Orbitals

According to Hund’s rule, atoms having a half-filled or fully-filled orbital are comparatively more stable, and more energy is required to remove an electron from such atoms. Therefore, the ionization energy of such atoms is relatively higher than expected normally from their position in the periodic table.

Half-filled and filled orbitals can create many regulations in ionization energy trends. For example, Be and N in the second period and Mg and P in the third period have slightly higher values of IE than the expected values.

• The higher values of IE of beryllium (Be → 2s²) and magnesium (Mg →3s²) are explained by the extra stability of the completely filled 2s orbital in Be and 3s orbital in Mg.
• Similarly, the higher values of IE of nitrogen (N → 2s² 2p³) and phosphorus (Mg →3s² 3p³) are explained by the extra stability of the half-filled 2p orbital in N and 3p orbital in P.

Shielding Effect and Ionization Energy

Electrostatic attraction between the electrons and nucleus shows that an outer electron is attracted by the nucleus and repelled by the electrons of the inner shell. The combined attractive and repulsive force acting on the outer electron experiences less attraction from the nucleus. It is called the shielding or screening effect.

The larger the number of electrons in the inner shell, the lesser the attractive force for holding the outer electron.

The radial distribution functions of the s, p, and d subshells show that for the same principal quantum number, the s-subshell is more shielding than the p-subshell and least shielding the d-orbital. Therefore, the shielding efficiency is in the following order:

ns orbital > np orbital > nd  orbital > nf orbital
Where, n = principal quantum number

Shielding Constant and Ionization Energy of Periodic Table Elements

Generally, when we move down in a group, the number of inner shells increases or the shielding constant increses, and hence the determined ionization potential tends is decrease.

Element of Group-2	Be	Mg	Ca	Sr	Ba
Atomic number	4	12	20	38	56
Shielding constant for valence electron	2.05	4.15	17.15	35.15	53.15
Ionization energy (kJ/mol)	899.5	737.7	589.8	549.5	502.9

Periodic Table Trends of Ionization Energy

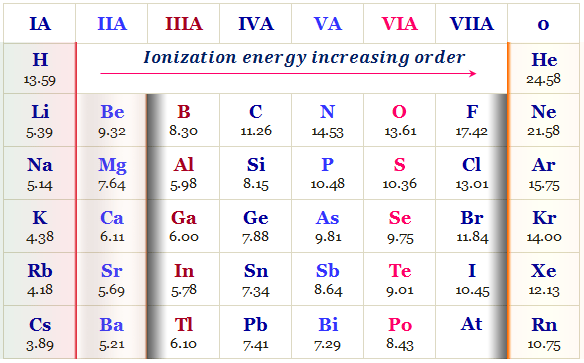
The greater the charge on the nucleus of an atom the more energy is required for removing an electron from the atom.

With the increasing atomic number electrostatic attraction between the outermost electrons and the nucleus of an atom increases. Therefore, the ionizing of an atom is difficult in chemistry. Hence ionization energy values generally increase in moving left to right in a period.

Ionization Energy of Second-Period Elements

Due to the presence of a fully-filled and half-filled orbital of beryllium and nitrogen, the ionization energy of beryllium and nitrogen is slightly higher than the neighbor elements boron and oxygen.

Therefore, the ionization potential trends of second-period elements maintain the following order,
Li < B < Be < C < O < N < F < Ne

Exceptions of Ionization Energy Trend

A few exceptions in the value of the ionization energy trends in the periodic table are explained based on the half-filled and fully-filled orbitals.

• Group-15 elements (nitrogen and phosphorus) in the periodic table have higher ionization potential than the group-16 elements (oxygen and sulfur).
• Similarly, group-2 elements (beryllium and magnesium) have higher than the group-13 elements (boron and aluminum) in the periodic table.

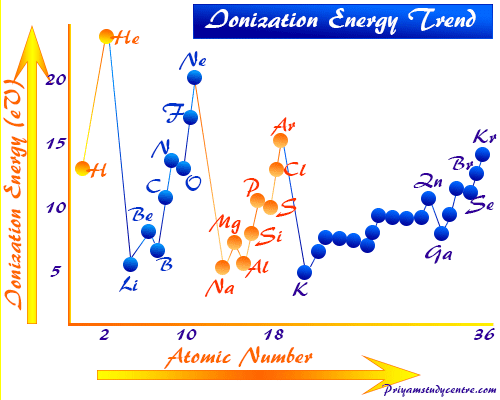
Ionization Energy of Nitrogen and Phosphorus

The measure first ionization energy of nitrogen greater than oxygen and phosphorus greater than sulfur.

Nitrogen and phosphorus in group-15 elements with atomic numbers 7 and 15. Therefore, the electron configuration of nitrogen and phosphorus are:

• Nitrogen (N): 1s² 2s² 2p³
• Phosphorus (P): 1s² 2s² 2p⁶ 3s² 3p³

From the above electronic configuration, the removal of an electron from half-filled 2p and 3p-orbital of nitrogen and phosphorus required more energy. Therefore, the IE of nitrogen is slightly greater than oxygen, and phosphorus is slightly greater than sulfur.

Beryllium and Oxygen

Removal of an electron from beryllium (Be) and magnesium (Mg) with a fully-filled s-orbital required more energy. Therefore, the ionization potential of beryllium is slightly greater than boron. Similarly, the ionization potential of magnesium is slightly greater than aluminum.

Positively Charged Ions

Ionization can be enormously influenced by the overall charge of the ionizing species such as M⁺, M⁺², M⁺³, etc. During ionization, electron withdrawal from a positively charged species is more difficult than from a neutral atom.

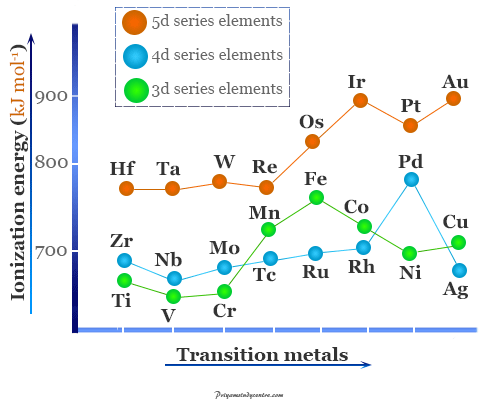
The first ionization potential chart of the elements varies with their positions in the periodic table. Among the periodic table elements, the noble gases have the highest ionization energy values and alkali metals have the lowest values.

Ionization Energy and Chemical Properties

In learning chemistry, the measure of ionization potential is an impotent chemical property of periodic table elements. We can explain various chemical properties with the help of ionization energies.

Ionization Energy and Chemical Reactivity

The lower value of ionization energies of alkali metals (lithium, sodium, potassium, rubidium, and cesium) suggest the highest reactivity of alkali metals. Similarly, the high value of ionization energies of noble gases suggests the low reactivity of noble gases.

Such rules are only applicable to metals that have high electropositive character but do not apply to highly electronegative elements. For example, the IE of fluorine is very high but fluorine is very reactive among periodic table elements.

Generally, highly reactive alkali metals and alkaline earth metals form polar molecules by ionic bonding with non-metals.

Reducing Properties of Elements

In redox reactions, the removal of an electron from an atom of a chemical element is called an oxidizing reaction. The element from where the electron is removed is called a reducing agent. The lower the value of the ionization potential, the greater its reducing power because it can easily remove electron from the element.

Basic Character and Ionization Potential

In chemical science, we can explain the acidic and basic character of elements by ionization energies. When the ionizing power of an element is lower, the basic character of such an element is greater but the acid character is lower.

The ionization energy measurement of periodic table elements can also be used to calculate various other chemical properties such as bond energy, electronegativity, electron affinity by Mulliken, etc.