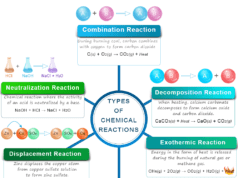
Zero Order Reaction Kinetics
Zero order reaction kinetics in chemistry define the rate of chemical reaction in terms of reactant and product per unit time. It is independent of the concentration of reacting species. Chemical kinetics deals with the speed and mechanism of reaction in terms of reactant and product molecules. In chemical equilibrium, only the initial and final states are considered. The relation between reactants and products is given from the Law of mass action and energy relation governed by thermodynamics Laws. It does not consider the time and intermediate states of a chemical reaction.
Example of Zero Order Reaction
The zero order reaction kinetics are rare in reality. Generally, the chemical reaction carried out by a chemical catalyst is in zero order. The enzyme catalysis reaction is an example of zero order reaction with respect to the substrate. In catalyzed reactions, the transformation takes place on the surface of the catalyst or the walls of the container.

The most common examples of zero-order sections are,
- The photochemical reaction between hydrogen with chlorine.
- Decomposition of nitrous oxide over a hot platinum surface.
- Decomposition of ammonia in the presence of molybdenum or tungsten surface.
- Dissociation of hydrogen iodide in the gold surface with high pressure. It is a bimolecular reaction.
Rate Law Expression
In kinetics, the rate of a chemical reaction is generally expressed in terms of reactant and product. Therefore, the concentration of reactant decreases, and the product increases. When these decrease or increase concentrations expressed per unit of time, we find the rate law in chemical kinetics.
A → Product
Rate of reaction = − d[A]/dt = k [A]n
In some surface reactions, the rate has been found to be independent of concentration. These reactions are known as zero order kinetics.
Zero Order Reaction Formula
Rate laws in chemical kinetics define the dependence of the concentration of the reacting species. Whereas the integrated law provides the increase or decrease of the concentration of reacting species at any time from the start of the reactions.
Integrated Rate Law for Zero Order Reaction
Let us take a chemical reaction with the initial concentration of reactant = a and product = 0. After time t concentration of reactant = (a − x) and product = x. Therefore, concentration decreases after t time = x.
The rate in terms of product,
dx/dt = k
where k = rate constant
or, dx = kdt
When we integrate the above equation within limits, produce the rate equation for the reactions,
x = kt + c
where c = integration constant
But when t = 0, that is the initial state of the reaction, x = 0. The integration constant (c) of the above equation is equal to zero.
∴ x = k × t
This is the formula that expresses the decreases or increases of concentration of the reactant or product within time.
Differential Form of Zero Order Reaction
Let the initial concentration of reactant = [A]0 and after t time = [A], thus the rate equation in terms of reactant,
− d[A]/dt = k × [A]0 = k
Negative sign because the concentration decreases with time and initial concentration reactant [A]0 = 0.
Again, − d[A] = kdt
Integrating the above equation
∫d[A] = k ∫dt
∴ − [A] = kt + c
where c = integration constant
If the initial concentration of the reactant = [A]0 when time = 0, that is the initial time,
− [A]0 = 0 + c
or, c = − [A]0
Therefore, the integrated rate equation for the zero order kinetics
− [A] = kt − [A]0
or, [A]0 − [A] = kt
It is another form of the rate equation for zero order kinetics.
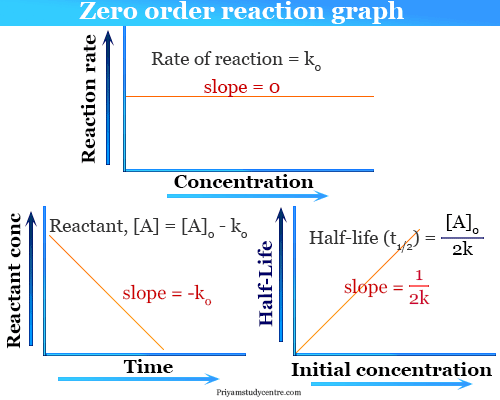
Zero Order Reaction Graph
The rate law formula for zero order reaction,
[A]0 − [A] = kt
When the rate of reaction is plotted against concentration and time, the following graph obtained below the picture,
Unit of Rate Constant
The rate equation for nth-order reaction = kn × [A]n
Therefore, the unit of rate constant,
kn = unit of concentration/(unit of concentration)n × unit of time = (unit of concentration)1−n/unit of time
Unit of Rate Constant for Zero Order Reaction
For zero order kinetics, n = 0 and molar concentration = mol lit−1.
Therefore, the unit rate constant for the zero-order reaction,
= (mol lit−1)1−0/s
= mol lit−1 s−1
Half life in Zero Order Reaction
Half life means 50 percent of reactants disappear in that time interval. When t = t½, that is the half-life of the reaction completed, the concentration of the reactant, [A] = [A]/2.
Therefore, [A]/2 = k × t½
or, t½ = [A]/2k
From the above formula, the half-life of the zero order kinetics depends on the initial concentration of the reactant.
Enzyme Catalyzed Reaction
Enzymes are complex protein produces by the living organisms of our environment. These are responsible for catalyzing infinite types of chemical changes occurring in our living system.
- For example, catalase obtained from living plant cells catalyzes the decomposition of hydrogen peroxide.
- Yeast contains various enzymes, among which maltase converts maltose into glucose, and zymase further converted glucose into ethyl alcohol.
All the reactions will be in zero order for a given amount of enzyme with respect to the substrate.
Factors Affecting Rate of Reaction
- The rate of the reactions is independent of concentration.
- Half-life is proportional to the initial concentration of the reactant.
- The rate of zero order kinetics in chemistry or chemical science is always equal to the rate constant at all concentrations.
Zero Order Reaction Problems
Problem: When is the rate of the reaction equal to the rate constant?
Solution: For zero order reaction, the rate of the reaction is equal to the rate constant or rate of reaction = k.
Problem: The half-life of zero order reaction = x. If the reaction is completed on t1 time, what is the relation between x and t1?
Solution: t½ = x = a/2k and completion time t1 = a/k. Therefore, x/t1 = (a/2k) × (k/a)
or, t1 = 2x