Radioactive Decay and Half Life
Radioactive decay is the spontaneous disintegration or emission of atomic particles like alpha, beta, gamma from the nuclei of radioactive substances in the form of nuclear energy. Therefore, radioactive decay is simply determined by counting the number of alpha, beta, and gamma radiation in a given time. Rutherford and soddy 1902 proposed the law of radioactive decay. According to them, atoms of radioactive elements undergo spontaneous disintegration to form a new atom of elements. Soddy also coined the term radioactive isotopes which occupy the same place in the periodic table. In chemistry, the half-life is the period of time when half of the radioactive substances undergo disintegration.
Radioactive Decay Formula
Radioactive decay is one important natural phenomenon obeying the first-order chemical kinetics. It is used mainly in radiocarbon dating and the determination of the age of matter or materials. The rate of the radioactive decay formula depends only on the single power of the radioactivity.
∴ dN/dt = − kN
Where N = number of the atoms of the disintegrating radioactive element, dt = time over which the decay is measured, and k = radioactive decay constant.
If N0 number of the atoms present at the time t = 0 and N number of atoms present after the time t. The radioactive decay formula is given below the picture,

Radioactive decay constant
From the above formula,
− (dN/N)/dt = k = rate constant
The quantity dN/N represents the fraction of the total number of atoms that disintegrate in time dt. Therefore, the radioactive decay constant represents the fraction of radioactive atoms that disintegrate in a unit time. The negative sign shows that N decreases with time.
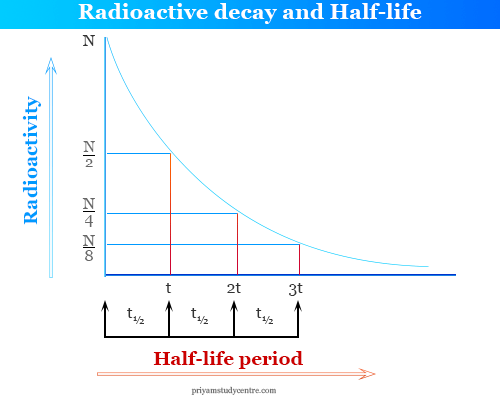
Half Life in Radioactivity
After a certain period of time, the value of (N0/N ) becomes one-half of the radioactive elements. This period of decay is called the half-life of radioactive material or substances. Half-life is a characteristic property of radioactive elements.
How to calculate half-life?
The radioactive decay formula,
ln(N0/N) = kt
When t = t½, N = N0/2,
t½ = ln2/k = 0.693/k
This equation provides the relation between half-life and radioactive decay constants. Hence the half-life is independent of the amount of the radio element present at a given time. The half-life of polonium-213 isotope = 4.2 × 10−6 sec and bismuth-209 isotope = 3 × 107 years.
If the radioactivity of an element is 100% and the half-life period of this element is 4 hours.
- After four hours, it decomposes 50% and the remaining 50%.
- After 8 hours it decomposed 75% and reaming 25% and the process continued.
- Hence, after complete n half-lives, the amount of radioactive element reaming (1/2)n.
Mean Life in Radioactivity
The mean life period of an atom of the radioactive element tells us the average span of time after which the atom will disintegrate. It is the length of time a radioelement can live before it disintegrates that may have values from zero to infinity. This explains the gradual radioactive decay of the radioisotopes instead of the decay of all the atoms at the same time.
The total number of radioactive atoms (N0) is composed of many small numbers of atoms like dN1, dN2, dN3, etc, each with its own life span t1, t2, t3, etc.
Mean Life and Half Life Relation
The mean life of radio-element is reciprocal of its radioactive decay constant in a nuclear reaction. This radioactive decay result can also be derived in a very simple way of learning chemistry or physics. The product of the mean life and disintegration constant is unity (tav × k = 1).
From the half-life and mean-life formula, we get the following radioactive decay equation,
t½ = 0.693/k = 0.693 tav
Application of Radioactive Decay
Carbon-14 Dating
Carbon-14 dating or carbon dating is a method for determining the age of organic compounds based on the accurate determination of the ratio of radioactive decay of carbon isotopes present in our environment.
The C-14 dating method was developed by Willard Libby, at the University of Chicago in 1940. He received a Nobel prize in chemistry or chemical science for his work in 1960. Carbon-14 is produced in the atmosphere by the interaction of neutron particles with ordinary nitrogen or cosmic reactions.
7N14 + +1e0 → 6C14 +1H1
Application of Carbon 14 Dating
Carbon reacts with atmospheric oxygen to form carbon dioxide and carbon dioxide is taken by plants in photosynthesis and by animals by eating plants. But when the animal or plant dies, it stops exchanging carbon with its environment. Since there is no fresh intake of stratospheric carbon dioxide and the dead matter is out of chemical equilibrium with the atmosphere.
The carbon-14 continues to decay so that thereafter a number of years only a fraction of carbon-14 is left on the dead matter. The ratio of carbon-14 and carbon-12 drops from the steady-state ratio in the living matter.
6C14 → 7N14 + -1e0 (t½ = 5760 years)
By measuring this ratio and comparing radioactive decay with living plants, we can estimate when the plant died or the age of dead substances.
How to Calculate Avogadro’s Number?
Let 1 g of radium-226 contain N number of atoms.
Therefore, N = N0/mRa
Where N0 = Avogadro number.
The mass number of radium = 226.
Then, k × N = k × (N0/mRa), where k = 0.693/t½.
In nuclear chemistry, one gram of radium-226 undergoes 3.7 × 1010 decay per second and half-life = 1590 years. The Avogadro number of radium-226 calculated from the radioactive decay law = 6.0 × 1023.
Age of Rock Using Half Life
Knowledge of the radioactive decay model of certain radioactive isotopes helps to determine the age of various rock deposits in nuclear chemistry. Let us consider uranium-containing rock formed many years ago. Generally, the radioactive uranium-235 started to decay and ended with lead-207 to form the decay series or chain.
The half-life of the intermediate members is small compared to that of uranium-235 (4.5 × 109 years). Therefore, uranium that started to decay many many years ago must have been completely converted to the stable lead-207 during this extra-long period.
Hence remaining uranium-235 and the lead-207 were present at zero time when the rock solidified. Therefore, both N0 and N are known. In radioactivity, the decay constant (k) is calculated from the knowledge of the half-life of uranium-235. Thus the age of the rock can be calculated.
Radioactive Decay Problems and Solutions
Problem: A piece of wood was found to have a carbon-14 and carbon-12 ratio of 0.7 times that in the living plant. Calculate the approximate period when the plant died (t₁/₂ = 5760 years).
Solution: We know that decay constant,
k = 0.693/t½
= 0.693/5760 years
= 1.20 ×10-4 yr−1
When we put the value, radioactive decay formula, the estimated time,
= (2.303 × 0.155)/(1.20 × 10−4) years
= 2970 years
Problem: A radioactive sample of uranium (t½ = 4.5 × 109 years) ore was found to contain 11.9 g of uranium-235 and 10.3 g of lead-207. How to calculate the age of the ore?
Solution: 11.9 g of uranium-238 = 11.9/238 = 0.05 mole of uranium and 10.3 g of lead-206 = 10.3/206 = 0.05 mole of lead-206. Therefore, the mole number of uranium-238 at zero time = (0.05+0.05) = 0.010 mole.
Decay constant = 0.693/(4.5 × 109 year)
= 0.154 × 10−9 yr−1
From the radioactive decay formula,
Time (t) = (2.303 × log2)/(0.154 × 10−9)
= 4.5 × 109 year