What is radioactivity?
Radioactivity is the phenomenon of emission of radiations as a result of the spontaneous decay of alpha, beta, and gamma particles from heavy atomic nuclei in the form of energy.
Radioactivity is a nuclear phenomenon connected with the instability of the nucleus. Therefore, radioactive decay is independent of pressure and temperature. It implies that the activation energy of radioactive decay is zero.
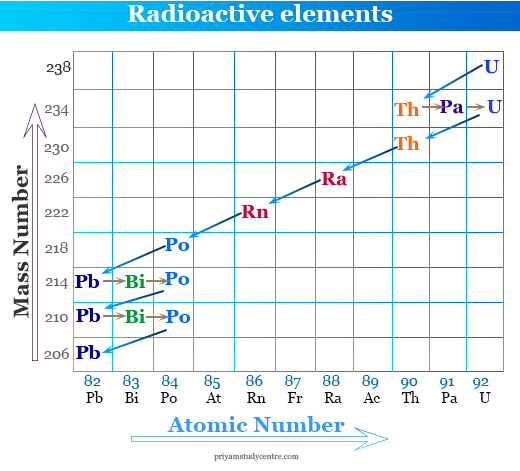
Atoms of radioactive elements spontaneously decay to form the atoms of new elements. Such nuclear reaction will be continued till a non-radioactive element is reached.
Measurement of radioactivity
In chemistry, radioactivity obeys the first-order decay reaction in chemical kinetics defined by counting the number of radioactive particles emitted in a given time. In practice, radioactivity expressed the number of disintegration per second.
Unit of radioactivity
One gram of radium undergoes about 3.7 × 1010 disintegrations per second. In radioactivity, the quantity of 3.7 × 1010 disintegrations per second is called one curie, which is the older unit of radioactivity.
Millicurie and microcurie are another units of radioactivity expressed by 3.7 × 107 and 3.7 × 104 disintegrations per second. The radioactive phosphorus-32, the beta emitter, has an activity of 50 millicuries per gram means every gram of phosphorus-32 is 50 × 3.7 × 107 decay taking place per second.
Becquerel to curie
SI unit of radioactivity is Becquerel or simply Bq. Becquerel is expressed by one disintegration per second and one curie = 3.7 × 1010 disintegrations per second. Therefore, 3.7 × 1010 Bq = 1 curie. Rutherford or simply Rd is the practical unit of radioactivity.
Discovery of radioactivity
Henri Becquerel discovery
In 1896 the French scientist Henri Becquerel discovered radioactivity of the substance potassium uranyl sulfate. He investigated the nature of electromagnetic spectrum radiation of x -rays which was discovered by Rontgen a few months earlier. He found that a photographic plate was shielded by a sample of potassium uranyl sulfate placed.
He obtains the conclusion that some particles emitting from the uranium compound could shield the cover of the photographic plate. The properties of alpha, beta, or gamma rays radiations were very similar to those of x -rays.
Marie and Pierre curie discovery
On April 20, 1902, Marie and Pierre Curie successfully isolate radioactive radium and polonium from ore pitchblende. Polonium or radium was much more radioactive than uranium. Therefore exceptional behavior of pitchblende was explained by this discovery.
In 1903, Pierre Curie was awarded the Nobel Prize in physics for her discovery. She shared this with Henri Becquerel and Marrie curie for their contribution to developing radioactivity.
In 1906, Pierre Curie died in a Paris street accident. After death, Marie won the Nobel Prize in chemistry for the discovery of the elements polonium and radium.
Cause of radioactivity
The nucleus of the radioactive elements is composed of two types of elementary particles like protons and neutrons. Therefore, the ratio of neutron/proton is the main cause of natural or artificial radioactivity. In radioactivity, the neutron/proton or n/p ratio helps to predict the stability of the nucleus of radioactive elements in chemical science.
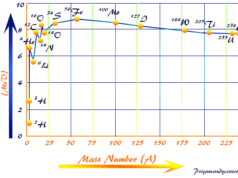
In learning chemistry or nuclear chemistry, the below graph is obtained by plotting the number of neutrons in the nuclei of stable isotopes against the respective number of protons.
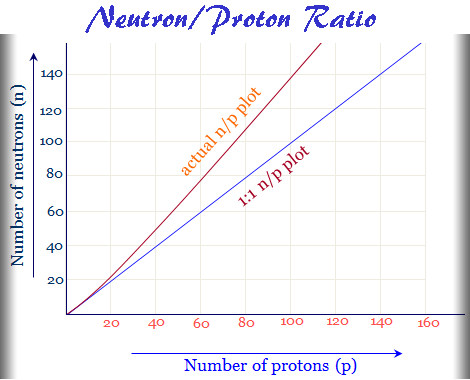
The above plot shows that the actual n/p plot of stable radioactive isotopes breaks off from the hypothetical 1:1 plot around an atomic number 20.
After atomic number 20, the line rises rather steeply. As the number of protons increases inside the nucleus, more and more neutrons are needed to minimize the proton-proton repulsion. Therefore, neutrons are served as the binding materials inside the radioactive nucleus.
Nuclear stability and radioactivity
Stability or instability in radioactivity is connected with the pairing of nuclear spins or nuclear charge. Since all the elements in the periodic table are not radioactive. Nuclear scientist studies these types of problems and connected the stability or instability of the nucleus with the pairing of nuclear spin.
- Nuclei with an even number of protons with an even number of neutrons are the most stable. Even number leads to spin pairing and odd number leads to unpaired spins.
- Nuclei with either proton number or neutron number odd are slightly less stable than even-numbered ones.
- The least stable radioactive isotopes are formed by an odd number of proton and an odd number of neutron.
Neutron to proton ratio
Neutron to proton ratio too high
Isotopes with too many neutrons in the nucleus can attain greater stability if one of the neutrons decays to form a proton. Such disintegration leads to the emission of an electron or beta rays,
0n1 → 1H1 + -1e0 (beta rays)
The neutron/proton ratio is high when the mass number of radioactive isotopes is greater than the average atomic weight of the element.
Neutron to proton ratio too low
A nucleus with a neutron to proton ratio too low attains nuclear stability by converting one proton to a neutron. Such a nuclear reaction is achieved either by the emission of a positron or by the capture of an electron. It occurs with a radioactive isotope whose mass number is less than the average atomic weight of the element.
Carbon-12 and carbon-14
The neutron/proton ratio for stable radioactive isotopes of carbon-12 = 1.0 with six protons and six neutrons. But for radioactive carbon-14 = 1.3 with eight neutrons and six protons. Therefore, caron-14 will show radioactivity by emitting beta rays from the nucleus.
Iodine-127 and iodine-133
The neutron/proton ratio for iodine-127 and iodine-133 = 1.4 and 1.5 respectively. Therefore, iodine-133 is a beta emitter largely used in nuclear medicine.
Problem: Why gold-197 is a non-radioactive substance but radium-226 is a radioactive substance?
Answer: The number of neutrons and protons is 188 and 79 respectively in gold-197. The neutron to proton ratio = 118/79 =1.49, which is less than 1.5. Therefore gold-197 is stable.
The number of neutrons and protons is 138 and 88 respectively in radium-226. Hence the neutron to proton ratio = 226/88 = 1.57, which is greater than 1.5. Therefore, radium-226 is a radioactive substance.
Positron emission
A nucleus deficient in neutrons will tend to attain nuclear stability by converting one of its protons to a neutron and this will be achieved either by the emission of a positron or by the capture of an electron. Positron emission occurs with light-type of radioactive isotopes which have a very low atomic number.
Positron emission example
Nitrogen-13 and iodine-121 has the neutron/proton ratio = 0.86 and 1.3 respectively. Therefore, these radioactive elements gain their nuclear stability by positron emission or electron capture reaction. But the electron capture reaction is not alike with positron emission reaction because radioactivity is a nuclear phenomenon.
| Positron emission |
| 1H1 → 0n1 + +1e0 (positron) |
| 7N13 → 6C13 + +1e0 |
| 53I121 → 52Te121 + +1e0 |
Electron capture equation
Orbital electron capture in radioactivity occurs with too-light isotopes of radioactive elements of relatively high atomic numbers. The nucleus of such atoms captures an electron from the nearest orbitals. Therefore, the orbital electron capture reaction in radioactivity changes one proton to the neutron.
| Electron capture equation |
| 37Rb82 + -1e0 → 36Kr82 |
| 79Au194 + -1e0 → 78Pt194 |
The effect of nuclear transformation resulting from the electron capture is the same as that with the positron emission reaction in radioactive transformation.
In both cases, the proton in the nucleus is converted into the neutron. The energy emission in such radioactive nuclear transformation is given the electromagnetic spectrum like x-rays.