Critical Constants of Gases
Critical constants like critical temperature (Tc), critical pressure (PC), and critical volume (VC) of gas in chemistry determine the condition and formula of liquefaction of real and ideal gases. The condition of liquefaction of real gases in learning chemistry is defined by Andrews’s isotherms and determined in terms of the van der Waals constant. Above the critical temperature, pressure, and volume gas molecules cannot be liquefied.
Most of the gases in our environment liquefy at ordinary pressure but the suitable lowering of cooling the temperature. However many gases like hydrogen, nitrogen, oxygen, and methane can not be liquefied at ordinary temperatures however high pressure may be used.
According to the kinetic theory, ideal gas can not be liquefied at critical temperature because the gas molecules are considered as point masses with no intermolecular attraction.
Real gases also, cannot be liquefied unless their temperature is below a certain value depending on the properties of gases. The temperature at which the gas can be liquefied is called its critical temperature.
Liquefaction of Gases
The condition of liquefaction and critical constants like temperature, pressure, and volume of real gas molecules are defined by Andrews’s isotherms and determined in terms of the van der Waals constant.
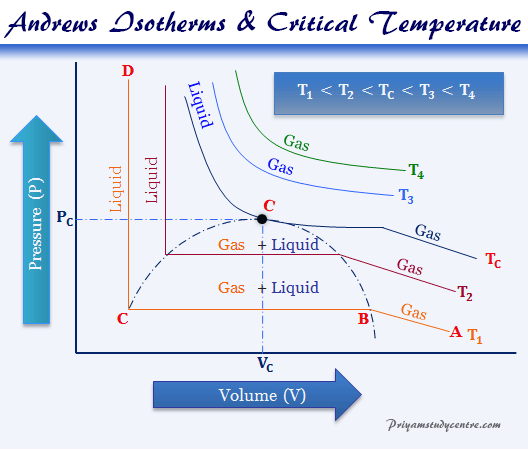
In 1869, Thomas Andrews carried out an experiment with a small quantity of carbon dioxide in a glass tube enclosed and sealed by the chemical element mercury. He studied P – V relations for carbon dioxide at different temperatures or the condition of liquefaction at the critical temperature.
At high temperatures or above the critical temperature the isotherms for liquefaction of carbon dioxide follow ideal gas law.
At low temperatures or below the critical temperature, the nature of the curves has altogether different appearances.
- As the pressures increase, the volume of the gas decreases in curves A to B. At this point, B liquefaction commences and the volume decreases rapidly as the gas is converted into a liquid with a much higher density.
- Point C, liquefaction of carbon dioxide is complete. The CD of the curve is evidence of this fact.
- AB represents the gaseous state, BC represents liquid or vapor in equilibrium, and CD shows the liquid state only.
- Still higher temperatures at T2, we get a similar type of curve to ABCD.
- At temperatures TC, the horizontal portion is reduced to a mere point, called the critical point or state of the gases.
Every gas can have a limited temperature above which it can not be liquefied.
Critical Temperature Pressure and Volume
The critical temperature, pressure, and volume simply represent TC, PC, and VC respectively, and above which the gases cannot be liquefied.
Critical Temperature
The Critical temperature (TC) is the maximum temperature at which the gas can be liquefied and the temperature above which the liquid cannot exist.
Critical Pressure
Similarly, critical pressure (PC) is the maximum pressure required for the liquefaction of gases at critical temperature.
Critical Volume
Critical volume (VC) is the volume occupied by one gram mole of gaseous substances at critical temperature and pressure.
Liquefaction of Gases and Critical Temperature
An examination of the PV curve at the temperature below the critical temperature may be discontinuous or break down during the transformation of gas to liquid. The continuity of the state of matter from the gas to liquid can be explained from the above Andrews isotherm ABCD at temperature, T1.
Suppose the gas is heated with the specific heat at constant volume along with AB. Then the gas gradually cooling at constant pressure along with BC, and the volume will be reduced considerably. On reaching D the process of liquefaction would appear.
At point D, the system contains highly compressed gas. But from the Andrews curve, the critical temperature point is the representation of the liquefaction point of the gases. Hence there is hardly a distinction between the liquid and the gaseous state. There is no line of separation between the two phases. This is known as the principle of continuity of the state.
Derivation of Critical Constants from Van der Waals Constant
With the increase in temperature, the minimum and maximum points come close to each other, and at the critical point (C) both maximum and minimum coalesce. The slope and curvature both become zero at this point.
In these conditions, we can calculate the critical constants (temperature, pressure, and volume) formula for real gases from the Van der Walls equation.
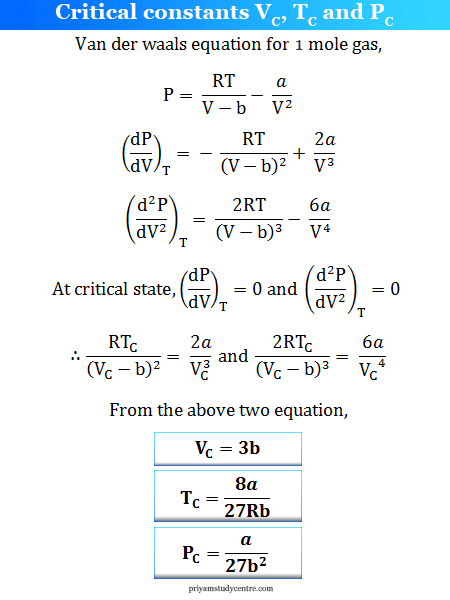
The measured value of VC, TC, and PC of gas,
- Critical volume (VC) = 3b
- Critical Temperature (TC) = 8a/27Rb
- Critical pressure (PC) = a/27b2
Question: Calculate the Van der Waals constant for the gas when critical temperature and pressure = 280.8 K and = 50 atm respectively.
Answer: a = 0.057 lit mol−1 and b = 4.47 lit2 atm mol−2
Real Gas Compressibility Factor
The compressibility factor formula of the gas,
Zc = PCVC/RTC
= 3/8
= 0.375
Critical coefficient value = 8/3 = 2.66
If we compare these values with the experimental values, we find that the agreement is very poor. Because Van der Waals equation at the critical state is not very accurate.
- The experimental value of the compressibility factor for non-polar or slightly polar bonding molecules like helium, neon, argon, oxygen, and methane is close to 0.29.
- For the molecules having polarity or polarization like chlorine, carbon disulfide, chloroform, and ethylene close to 0.26 or 0.27.
- For hydrogen bonding molecules like ammonia, water, and methyl alcohol are close to 0.22 to 0.24.
Van der Waals Equation and Critical Constants
Van der Waals equation for real gas can be derived from the critical constants formula (temperature and pressure). Critical volume in the expression avoided due to the difficulty of determination. From the critical constants like temperature, pressure, and volume in terms of Van der Waals constants,
- b = VC/3
- a = 27 R2 TC2/64PC
Problem: The critical constants for water are 647 K, 22.09 MPa, and 0.0566 dm3 mol−1. What is the value of a and b?
Solution: TC = 647 K, PC = 22.09 Mpa = 22.09 × 103 kPa, VC = 0.0566 dm3 mol−1.
Therefore, Van der Waals constant,
b = VC/3
= (0.0566 dm3 mol−1)/3
= 0.0189 dm3 mol−1
From the critical constants formula of real gas,
a = 3 PC VC2
= 3 (22.09 × 103) × (0.0566)2
= 213.3 kPa mol−2
Question: An atom in the molecule has TC = −122 °C, PC = 48 atm. What is the radius of the atom?
Answer: Calculated radius of the atom = 1.47 × 10−8 cm.
Critical Temperature of Ideal Gas
For an ideal gas a = 0, since there exist no forces of attraction between the molecules. Therefore, the TC of such gases is equal to zero. Hence the elementary condition for liquefaction of ideal gases is to cool below the critical temperature.
The ideal gas can not be liquefied at the critical temperature or zero Kelvin because practically not possible to attain zero Kelvin temperature.
