Dipole Moment Molecules

Dipole Moment of Benzene Molecule

Dipole moment of benzene molecule is zero suggesting that the benzene ring has a regular hexagonal planner aromatic structure with sp² hybridized atomic orbitals in the carbon atom. The dipole moment of benzene and substituted benzene molecules are calculated by different theoretical or experimental formulas in chemistry.

The aromatic hydrocarbon benzene was first isolated by Faraday in 1825 in cylinders of the compressed illuminating gas molecule from the pyrolysis of whale oil.

In learning chemistry, substituted benzene molecule shows aromatic properties with (4n + 2)π electrons. The chemical bond in the benzene molecule has double bond properties with five canonical structures having different bond energy.

Benzene derivatives

If a hydrogen atom in the benzene ring is substituted by another atom or group, this molecule acquires bond polarity. Examples of such benzene derivatives which show dipole moment are chlorobenzene, nitrobenzene, phenol, benzyl alcohol, etc.

The dipole moment of o, p, m-isomers of the benzene ring can be calculated from the formula,
μ² = m₁² + m₂² + 2 m₁m₂ cosθ.

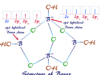
Ortho para meta position in benzene ring

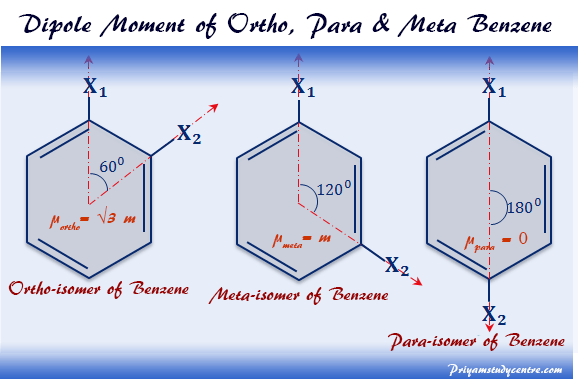
When one group or element introduces into the ring, only one product is produced. The ortho, para, meta, or o, p, m isomers are formed by the introduction second group in the benzene ring given above the picture.

The dipole moment of ortho isomer of benzene molecule will have the highest value and p isomer has the lowest value equal to zero like methane.

Dipole moment and structure of molecules

The resultant dipole moment of molecules is equal to the vectorial sum of individual bond or group moments. It depends on the structure of the molecules.

The dipole moment of the di-substituted molecules like xylene, dichlorobenzene, and dinitrobenzene can be calculated by the vectorial addition formula,
μ² = m₁² + m₂² + 2 m₁m₂ cosθ
where m₁ and m₂ are individual group moments
θ = angle at which m₁ and m₂ are inclined to each other

Dipole moment of xylene

Ortho, para, and meta-xylene are the substituted derivatives of benzene having the molecular formula C₆H₄(CH₃)₂.

Dipole moment of o-xylene

For o-xylene molecule, the groups moment of CH₃ group = m and θ = 60°.

From dipole moment formula,
μ²_o-xylene = 2m²(1 + cos60°)
= 3m²
∴ Dipole moment of o-xylene = √3m

Dipole moment of p-xylene

For o-xylene molecule, θ = 180°.

From dipole moment formula,
μ²_p-xylene = 2m²(1 + cos180°)
= 0
∴ Dipole moment of o-xylene = 0

Dipole moment of m-xylene

For o-xylene molecule, θ = 120°.

From dipole moment formula,
μ²_p-xylene = 2m²(1 + cos120°)
= m²

Therefore, the dipole moment of o-xylene = m. From the above three calculations, the dipole moment di-substituted molecules of a benzene ring or xylene, μ_ortho > μ_meta >μ_para.

Similar way, we can calculate the dipole moment of o, p, and m-dinitrobenzene or dichlorobenzene.

Dipole moment of 1, 3, 5 trinitrobenzene

1, 3, 5 trinitrobenzene being symmetrical non-polar molecule. When it is dissolved in benzene, a charge transfer bonding involves some kind of donner acceptor interaction.

Due to the formation of charge-transfer complexes in the C₆H₆ solution, the compound shows a significant dipole moment.

Problem: If dipole moment of o-xylene molecule = 0.693D, calculate the μ for toluene molecule.

Answer: For o-xylene, θ = 60° and μ = √3 m.

∴ m_xylene = 0.693/√3
= 0.4D

Again for toluene, θ = 120°
∴ μ_toluene = 0.4D

Problem: Why p-dinitrobenzene has μ = 0 but para – dihydroxybenzene μ ≠ 0?

Answer: In p-dinitrobenzene, the substituted nitro group is the same plane of the benzene ring but in p-dihydroxybenzene, the substituted hydroxy groups are not on the same plane.

Among these two substituted molecules, the dipole moment of p-dinitrobenzene is zero but the p-dihydroxybenzene molecule is polar.