Polarity of Bonds and Polar Molecules
Polarity of bonds and polar molecules are formed by the asymmetric charge distribution on chemical bonds. Water, hydrogen chloride, ammonia, nitrobenzene, and alcohol are common examples of polar molecules. Polar and non-polar molecules are composed of positively charged nuclei and negatively charged electron particles distributed in space. The dipole moment is an important tool for determining the structure of polar or nonpolar molecules.
The determination of bond polarity for learning chemistry is given from the dipole moment chart for polar and non-polar molecules.
Polar and Non polar Molecules
- Non-polar molecules: When the center of gravity of positive and negative charges coincide, the molecules are called non-polar. Hence the dipole moment of molecules like hydrogen, chlorine, carbon dioxide, methane, and benzene is zero.
- Polar molecules: On the other hand, hydrogen chloride, chloromethane, chloroform, nitrobenzene, water, and ammonia are polar molecules but the polarity of the individual chemical bonding may be present or absent.
The electric polarization of chemical substances arises when non-polar molecules are placed between positive and negative plates of the electric field.
The polarity of the molecule is quantitatively expressed by the term dipole moment. It helps to determine the molecular size and shape, spatial arrangement, bond polarity, bond energy, and residue charge on the atoms.
Examples of Nonpolar Covalent Molecules
Binary homonuclear diatomic molecules are non-polar or polarity equal to zero because the bonding chemical elements possess the same electronegativity.
The polarity of homonuclear diatomic molecules like hydrogen, nitrogen, oxygen, chlorine, bromine, and iodine is zero. The bonding electrons of these molecules are shared equally by the two nuclei. These types of bonds are called non-polar covalent bond.
Examples of Polar Covalent Molecules
According to the above rule, heteronuclear diatomic molecules show polarity due to their electronegativity and ionization energy differences.
The electronegativity difference is not only the tool to determine the polarity of the molecule. Therefore, to decide the polarity of heteronuclear molecules need to learn the composition and geometry.
Hence carbon dioxide, carbon disulfide, beryllium chloride, and phosphorus pentachloride are non-polar. The bonding atoms of these molecules have different electronegativity and electron affinity.
What is Polarity in Chemistry?
Polarity arises when the center of gravity of the positive charge does not coincide with the center of gravity of the negative charge. For example, polar covalent molecules like Hydrogen chloride, water, ammonia, and chlorobenzene show polarity in chemistry.
Beryllium chloride is linear with a bond angle of 180° but the water molecule is non-linear with a bond angle of 104°.
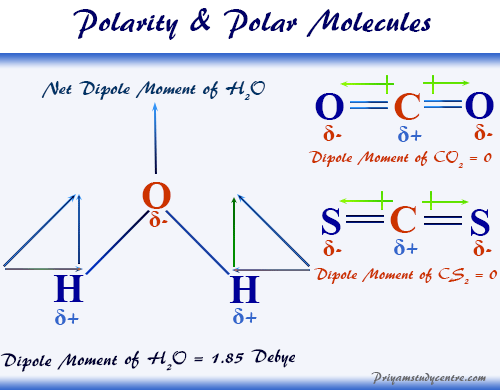
Polarity of Water
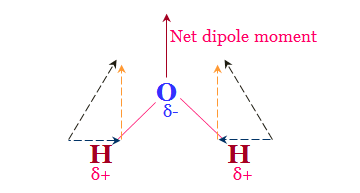
The excited-state electronic configuration of the central oxygen atom of water is 2s2 2px2 2py1 2pz1.
One s- and three p-orbitals of oxygen combine to form sp3-hybridized orbitals. Therefore, a water molecule is formed by the tetrahedral arrangement of two lone pairs and two two bond pairs.
For calculating the polarity of water, we find two contributions like electronegativity difference between oxygen and hydrogen and lone pairs of electrons.
How to Determine Bond Polarity?
The determination of dipole moment and polarity is given by the product of charge and distance of the separation or bond length.
When +q amount of positive charge separates by −q of negative charge and l is the distance between two centers of the molecule, dipole moment,
µ = q × l
Perfectly non-polar substances show zero dipole moment and polar molecules have positive values. The determination of the dipole moment helps to predict the polarity of the molecule.
| Molecules | Dipole moment | |
| Carbon dioxide | Non-polar molecules | 0 Debye |
| Carbon disulfide | 0 Debye | |
| Carbon tetrachloride | 0 Debye | |
| Boron trichloride | 0 Debye | |
| Water | Polar molecules | 1.85 Debye |
| Hydrogen sulfide | 1.10 Debye | |
| Ammonia | 1.46 Debye | |
| Nitrogen trifluoride | 0.20 Debye | |
Unit of Dipole Moment
The charge of an electron = 4.8 × 10−10 esu and the distance between the center is of order 10−8 cm.
Hence the calculated dipole moment order,
= 10−10 × 10−8
= 10−18 esu
= 1 Debye
∴ 1 Debye = 10−18 esu cm
= 3.336 × 10−30 coulomb meter
Dimension of Dipole Moment
Unit of µ = unit of charge × unit of length
Therefore, the CGS unit of dipole moment = esu × cm
According to Coulomb’s Law,
F = q1q1/Dr2
Therefore, (esu)2 = dyne × cm2
= g cm sec−2 × cm2
The dimensions of dipole moment = M1/2 L5/2 T−1.
Question: P-F, S-F, Cl-F, and F-F which of the following chemical bonds show the lowest polarity?
Answer: The electronegativity or electron affinity difference between the two fluorine atoms is equal to zero. Therefore, the dipole moment of the fluorine among these molecules is zero.
Polarity of Organic Compounds
All the saturated hydrocarbons of our environment like methane, ethane, propane, and butane are found to be non-polar or zero polarity.
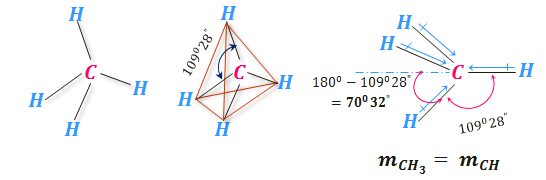
Polarity of Methane Molecule
The non-polar character of methane is easily understood from the symmetrical tetrahedral structure with the carbon atom at the center and four identical valencies making an angle of 109.5°.
The absence of polarity in methane molecules implies the carbon-hydrogen bond moment balancing the net moment contributed by the remaining three carbon-hydrogen bonding.
The experimental calculation of the bond moment or polarity of the alkyl group = 0.04 debye equal to the bond moment of the carbon-hydrogen bond. Not only alkyl groups but the radicals have also definite chemical bonding moments called group moments.
When a hydrogen atom in a different saturated hydrocarbon is replaced by a hydroxyl group to produce homologous alcohols, all of the latter should have the same polarity but the molecules are polar.
