Balancing Chemical Equations

Balancing Chemical Equations

Balancing chemical equations by ion-electron formula and change of oxidation number are used to balance the oxidation reduction process or redox reactions for learning chemistry.

• The ion-electron method is set up by balancing the partial equations of oxidant and reductant and balances the charges of these partial equations in acids and bases solution.
• In the oxidation number method, the changes in oxidation numbers of reactant and product atoms present in chemical elements, molecules, or ions are used for balancing chemical equations in chemistry.

The balancing of a chemical equation is based on the law of conservation of mass. According to the law of conservation of mass, ‘mass can neither be created nor be destroyed during a chemical reaction’. Similarly, the number of atoms of each chemical element remains the same before and after a chemical reaction.

Balancing Redox Reactions by Ion Electron Method

Balancing chemical equations by the ion-electron method has certain general rules or formulas that we use to balance redox reactions. We use rules for balancing equations by the ion-electron method may include,

• Certain the oxidizing agent and reducing agent, and their chemical formula for balancing chemical equations.
• Set up the partial balancing equations representing the reduction of the oxidant and the oxidation of the reductant.
• If the reaction occurs in an acid solution, a requisite number of hydrogen ions for balance the number of atoms involved in the partial equations. For the alkaline solution or high pH solution, we use hydroxyl ions.
• Balancing the changes of partial chemical equations by adding a suitable number of electrons. These electron particles are involved in balancing half-reactions.
• Multiply each partial equation by a suitable factor for balancing ionization chemicals. Each of the two partial equations involves the same number of electrons.
• Add the partial equations and cancel out similar species that appear on both sides of the balancing chemical reaction.

Examples of Balancing Chemical Equations

Balancing Fe in KMnO₄ Solution

Potassium permanganate in dilute sulfuric acid oxidizes iron from the ferrous state to the ferric state by changing the electronic configuration of the iron atom. Permanganate ion is the oxidant and the ferrous ion is the reductant in balancing chemical equations.

MnO₄⁻ + H⁺ + Fe⁺² → Mn⁺² + Fe⁺³ + H₂O

The left-hand side of the ultimate equation will carry MnO₄⁻, H⁺ ion, and Fe⁺² ions, and the right-hand side will have Mn⁺², water, and Fe⁺³.

The partial equation represents the reduction of the oxidant,

MnO₄⁻ → Mn⁺²

This reaction occurs in an acid solution, thus we use hydrogen ions to balance the four oxygen atoms in the permanganate ion,

MnO₄⁻ + 8 H⁺ → Mn⁺² + 4 H₂O

The above partial equation is still unbalanced from the viewpoint of charges. The equation balances by bringing in five electrons,

MnO₄⁻ + 8 H⁺ + 5 e⁻ → Mn⁺² + 4 H₂O

The partial equation represents the oxidation of the reductant,

Fe⁺² → Fe⁺³ + e⁻

It is a balanced equation for charges and reacting elements. To balance the charges of partial equations, this equation multiplies by 5 and is added to the first equation.

MnO₄⁻ + 8 H⁺ + 5 e⁻ → Mn⁺² + 4 H₂O
5 × ( Fe⁺² → Fe⁺³ + e⁻)
MnO₄⁻ + 8 H⁺ + 5 Fe⁺² → Mn⁺² + 5 Fe⁺³ + 4 H₂O

Balancing Potassium Iodide in Acid Solution of Dichromate

For balancing the oxidation of potassium iodide in an acid solution of dichromate, chromium reduces from the +6 state to the +3 state, and the iodine ion is oxidized to form the elementary iodine molecule.

The balancing partial equations of the dichromate side and iodine side are,

Cr₂O₇⁻² + 14 H⁺ + 6 e⁻ → 2 Cr⁺³ + 7 H₂O
2 I⁻ → I₂ + 2 e⁻

For balancing overall equations iodine side multiplies by 3 and is added to the dichromate side.

Cr₂O₇⁻² + 14 H⁺ + 6 e⁻ → 2 Cr⁺³ + 7 H₂O
3 (2 I⁻ → I₂ + 2 e⁻)
Cr₂O₇⁻² + 14 H⁺ + 6 I⁻ → 2 Cr⁺³ + 3 I₂ + 7 H₂O

Permanganate Ion in Alkaline Solution

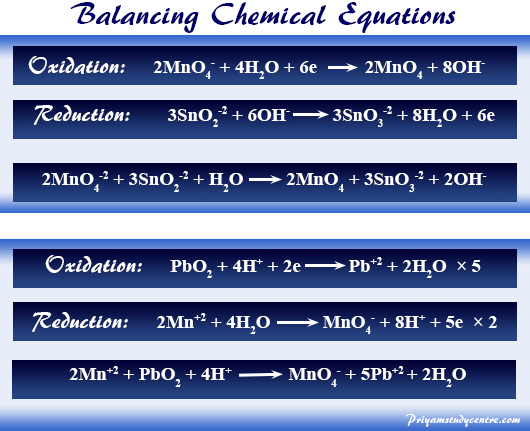
Permanganate ion in an alkaline solution oxidizes Na₂SnO₂ to Na₂SnO₃. The partial equation represents the reduction of oxidants in an alkaline solution and balances the chemical equations with a requisite number of OH⁻ ions.

MnO₄⁻ + 2 H₂O → MnO₂ + 4 OH⁻

The above partial equation is still unbalanced from the viewpoint of charge, the equation is balanced by bringing in three electrons.

MnO₄⁻ + 2 H₂O + 3 e⁻ → MnO₂ + 4 OH⁻

Again the partial equation represents the oxidation of the reductant.

SnO₂⁻² + 2 OH⁻ → SnO₃⁻² + H₂O + 2 e⁻

For balancing overall chemical equations, the first partial equation multiplies 2, and the second partial equation multiplies 3.

2 MnO₄⁻ + 4 H₂O + 6 e⁻ → 2 MnO₂ + 8 OH⁻
3 SnO₂⁻² + 6 OH⁻ → 3 SnO₃⁻² + 3 H₂O + 6 e⁻
2 MnO₄⁻ + 3 SnO₂⁻² + H₂O → 2 MnO₂ + 3 SnO₃⁻² + 2 OH⁻

Permanganate to Manganous by Hydrogen Peroxide in Acid Solution

Balance partial equations for the above chemical reaction are,

MnO₄⁻ + 8 H⁺ + 5 e⁻ → Mn⁺² + 4 H₂O
H₂O₂ → 2 H⁺ + O₂ + 2 e⁻

Balancing the overall charges, the first equation is multiplying by 2 and the second equation multiplying by 5.

2 MnO₄⁻ + 16 H⁺ + 10 e⁻ → 2 Mn⁺² + 8 H₂O
5 H₂O₂ → 10 H⁺ + 5 O₂ + 10 e⁻
2 MnO₄⁻ + 5 H₂O₂ + 6 H⁺ → 2 Mn⁺² + 8 H₂O + 5 O₂

Balancing Equations Practice Problems

Problem: How can we balance the equation for the oxidation of Mn⁺² to MnO₄⁻ by acidic NaBiO₃?

Solution: NaBiO₃ oxidizes Mn⁺² to MnO₄⁻ in sulfuric acid solution with the formation of BiO⁺ ion.

Balancing partial equations and overall chemical equations for the above chemical reaction are

2 Mn⁺² + 8 H₂O → 2 MnO₄⁻ + 16 H⁺ + 10 e⁻
5 BiO₃⁻ + 20 H⁺ + 10 e⁻ → 5 BiO⁺ + 10 H₂O
2 Mn⁺² + 5 BiO₃⁻ + 4 H⁺ → MnO₄⁻ + 5 BiO⁺ + 2 H₂O

Problem: Balancing the chemical equation of reduction of nitrate ion to ammonia by aluminum in aqueous sodium hydroxide.

Solution: The Balance partials and overall equation for the reduction of nitrate ion to ammonia by aluminum in an aqueous sodium hydroxide are

3 NO₃⁻ + 18 H₂O + 24 e⁻ → 3 NH₃ + 27 OH⁻
8 Al + 32 OH⁻ → 8 AlO₂⁻ + 16 H₂O + 24 e⁻
3 NO₃⁻ + 8 Al + 2 H₂O + 5 OH⁻ → 3 NH₃ + 8 AlO₂⁻

Balancing Chemical Equations by Oxidation Number Method

Oxidation and reduction reactions go hand in hand during a chemical reaction. We can specify oxidation or reduction by the change of oxidation number of an element from reactant to product.

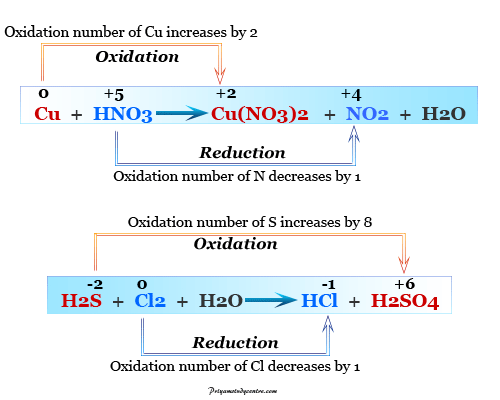
For balancing chemical equations, the change of oxidation number can be used for oxidation and reduction reactions (redox reactions). It is called balancing equations by oxidation number method.

For example, we can use the oxidation number method for balancing equation where iron can be oxidized by acidic permanganate solution

MnO₄⁻ + Fe⁺² → Mn⁺² + Fe⁺³

The oxidation number of Mn decreases by 5, and iron increases by 1 in the above equation. For equalizing the increase and decrease in oxidation number, we can put the right factor in the above equations,

MnO₄⁻ + 5 Fe⁺² → Mn⁺² + 5 Fe⁺³

For balancing the overall equation, we use hydrogen ions and water molecules.

MnO₄⁻ + 8 H⁺ + 5 Fe⁺² → Mn⁺² + 5 Fe⁺³ + 4 H₂O

Examples of Balancing Equations by Oxidation Number Method

Balancing Iodide Ion in Acidic Dichromate Solution

The chemical equation of iodide ion and acidic dichromate solution,

Cr₂O₇⁻² + I⁻ → 2 Cr⁺³ + I₂

In the above equation, the oxidation number of chromium decreases by 3, and the oxidation number of iodine increases by 1. After putting the right factor for equalizing the increase and decrease in oxidation number,

Cr₂O₇⁻² + 6 I⁻ → 2 Cr⁺³ + 3 I₂

Fourteen hydrogen ions and the requisite number of water molecules are needed to balance the overall equation. Therefore, the overall balanced equation is,

Cr₂O₇⁻² + 6 I⁻ + 14 H⁺ → 2 Cr⁺³ + 3 I₂ + 7 H₂O

Balancing Sodium Stannite to Stannate in Alkaline Solution

The chemical equation where stannite transforms to stannate in the presence of permanganate,

MnO₄⁻ + SnO₂⁻² → MnO₂ + SnO₃⁻²

The oxidation number of manganese decreases by 3 and the oxidation number of tin increases by 2. After equalizing the increase and decrease in oxidation number by putting the right factor,

2 MnO₄⁻ + 3 SnO₂⁻² → 2 MnO₂ + 3 SnO₃⁻²

Two hydroxyl ions and the requisite number of water molecules are added to balance the above chemical equation. Therefore, the balancing equation for the above reactions,

2 MnO₄⁻ + 3 SnO₂⁻² + H₂O → 2 MnO₂ + 3 SnO₃⁻² + 2 OH⁻

Balancing Iodide Ion and Iodate Ion in Acid Solution

The change of oxidation number of iodine to balancing iodide ion and iodate ion in acid solution,

I⁻ (−1) + IO₃⁻ (+5) → I₂ (0)

The oxidation number of iodide increases by 1 and the iodate ion decreases by 5. Putting the right factors for decrease and increase in oxidation number and balancing the above equation,

I⁻ + IO₃⁻ + 6 H⁺ → I₂ + 3 H₂O

Balancing Sulfurous Acid in Dichromate Ion

Balancing chemical equations for the oxidation of sulfurous acid to sulfuric acid by potassium dichromate is,

3 SO₃⁻² + Cr₂O₇⁻² + 8 H⁺ → 3 SO₄⁻² + 2 Cr⁺³ + 4 H₂O

For balancing equations, the oxidation number of two chromium atoms decreases by 6, and the oxidation number of sulfur increases by 2. Therefore, we put the right factor and the requisite number of hydrogen ions and water to balance the above ionic equations.

The methods used for balancing all the above chemical reactions are carried out by the ion-electron formula and oxidation number method. We also used the hit-and-trial method to balance the various chemical equations.

In learning chemistry or chemical science, the above types of balancing methods or formulas are used only to balance oxidation-reduction or redox reaction reactions.