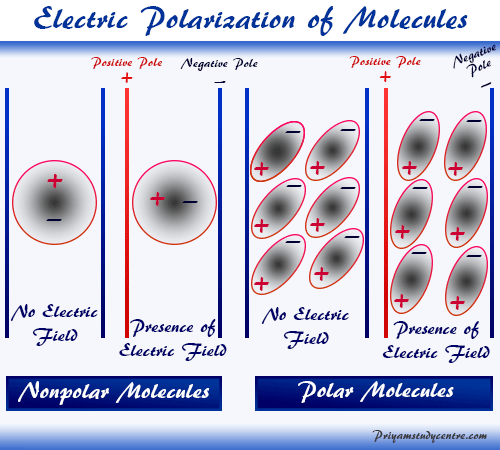
What is Electric Polarization?
Electric polarization occurs when a non-polar molecule is placed between two parallel plates with an applied electric field. The electric field tends to attract the negatively charged particles or electron clouds towards the positive plate and the positive charge nucleus towards the negative plate. In the presence of an electric field or current, there will be observed an electrical distortion or polarized molecule to form an electrical dipole. In learning chemistry or physics, such a type of distortion process in the molecules is called electric polarization. The polarization disappears as soon as the polarized field is withdrawn and the polarizing molecule comes back to its original state.
Types of Electric Polarization
There are two main types of polarization of molecules,
- Induced polarization
- Orientation polarization
Induced Polarization
Let induced electric polarization = Pi and induced dipole moment = µi. The induced dipole moment or simply the induced moment is directly proportional to the strength of the electric field applied(F).
Therefore, μi ∝ F
When electric force is very low, otherwise, hyperpolarization may occur among the polarized molecules.
μi = αi F
Where αi = proportionality constant. This constant is called the induced polarizability constant of the polarizing molecule.
The induced electric polarization in chemistry means the amount of induced moment in the polarized molecule when the unit electric field of current strength is applied.
Orientation Polarization
When an electric field produces polarized molecules, the dipolar molecules tend to orient in the direction of the field. This is called orientation polarization. It expresses as,
P0 = 4πN0α0/3
Where α0 = orientation polarisability
Debye calculated the value of α0 = μ2/3KT.
Hence the total polarization (Pt) = Pi + P0
However, the orientation of chemical elements has two tendencies. Polarized molecules tend to orient in the direction of the applied field (applied). Thermal energy or specific heat tends to destroy the alignment of the molecules.
Electric Polarization Formula
Mossotti derived a relation between the polarizability of substances and the dielectric constant of the non-polar medium between two plates from electromagnetic theory.
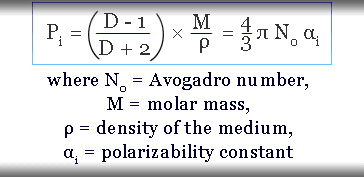
Induced polarizability constant and given when the distortion is produced in the 1 mole of the polarizing substance by a unit electric field. Therefore, the electric polarization constant formula for a given molecule and independent of temperature for learning chemistry or physics.
Unit of Dielectric Constant
Dielectric constant (D) = C/C0
Where C = capacitance of the condenser containing the polarized substance and C0 in the vacuum. Hence the dielectric constant is a dimensionless quantity having the value unity for vacuum. Other substances value of the dielectric constant is greater than unity.
The induced dipole moment of the crystalline solid, liquid, and gas substance is calculated by measuring the dielectric constant, density (ρ), and molar mass (M) of the polarized substance.
Unit and Dimension of Polarization
From the definition and polarizing formula, we can prove that the electric polarization constant has the dimension of the volume. Unit of dipole moment = esu × cm and force unit = esu cm−2, obtained from Coulomb’s law.
Therefore, the unit of electric polarization constant (αi)= r3, where r = radius of the polarized molecule assuming it to have a spherical shape.
The polarizability of the atom increases with the increasing atomic size, atomic number, and ionization energy of polarizing substances. Hence the atom behaves like a dipole and this dipole moment is induced by the applied electric field.
Debye Equation
For the examples of polarized molecules like methyl chloride, water, and hydrogen fluoride the molar electric polarization is not constant. It decreases with increasing temperature. Therefore, the Clausius Mossotti equation fails very badly for the polarity of the bond. The reason for the failure of the equation is put forward by P Debye for molar polarization.
According to him, when an electric field is applied between two linear parallel plates containing polarized gas molecules, two effects will occur, induced and orientation polarization. Here induced polarization tends to increase the induced moment among the molecules which discuss broadly before.
Electric Polarization Examples
A polarize chemical bond is fixed and unable to orient in a fixed direction. Therefore, the orientation polarization equal to zero. Hence for the condensed system where strong intermolecular forces prevent the free rotation of the polarized molecules.
At very high temperatures tending to infinity,
1/T = 0 and Pt = 0
Therefore, Pt = Pi
For example, experimental determination for molar electric polarization of many substances like carbon dioxide (greenhouse gas), and hydrocarbons like methane, ethane, propane, nitrogen, and hydrogen remains constant and does not vary with temperature.
But in many examples of polarized molecules like hydrochloric acid, methyl chloride, nitrobenzene, benzyl alcohol, etc the molar electric polarization is dependent on temperature.